3. 攻击算法基础¶

“攻击是为了更好的防御。” 一个有效的攻击算法可以帮助识别模型的弱点，进而启发更好的防御策略。本章节将介绍几种常见的攻击类型及其代表性算法，包括对抗攻击、数据投毒、后门攻击、模型抽取、数据抽取和成员推理攻击。这些算法主要在过去十年中针对小模型（如CNN、ResNet-18、ResNet-50等）提出，揭示了不同阶段、维度和攻防设置下的安全问题，为后续大模型安全讨论奠定了基础。尽管大模型在结构和复杂度上有所不同，但本质上仍是神经网络，因此许多针对小模型的攻击算法同样适用于大模型。通过研究这些基础攻击算法，我们能够更好地预测和防范人工智能模型在实际应用中可能面临的安全威胁。

3.1. 对抗攻击¶

“对抗样本”这一概念最早由Biggio等人 (Biggio et al., 2013) 和Szegedy等人 (Szegedy et al., 2014) 于2013年提出。Biggio等人首次发现攻击者可以通过恶意操控测试样本来绕过支持向量机（SVM）和浅层神经网络的检测，这种攻击被称为“躲避攻击”（evasion attack）。Szegedy等人则对深度神经网络提出了类似的攻击，定义为对抗样本（adversarial example），并将生成对抗样本的过程称为对抗攻击（adversarial attack）。

对抗攻击是一种针对机器学习模型测试阶段的攻击方法。它通过在干净测试样本\({\boldsymbol{x}} \in X \subset \mathbb{R}^d\)中添加细微噪声，构造对抗样本\({\boldsymbol{x}}_{adv}\)，从而误导模型\(f\)做出错误预测。为了提高对抗攻击的隐蔽性，通常会使用扰动约束\(\|{\boldsymbol{x}}_{adv} - {\boldsymbol{x}}\|_p \leq \epsilon\)将对抗样本\({\boldsymbol{x}}_{adv}\)限制在干净样本\({\boldsymbol{x}}\)的周围，其中\(\|\cdot\|_p\)表示向量的\(L_p\)范数，\(\epsilon\) 是扰动上限（或称扰动半径）。这一范数约束体现了对抗样本的重要特点，即在视觉上与干净样本没有明显差异，因为添加的噪声“微小且不可察觉”。然而，随着攻击算法的发展，也出现了无约束的攻击方法，例如物理对抗补丁。

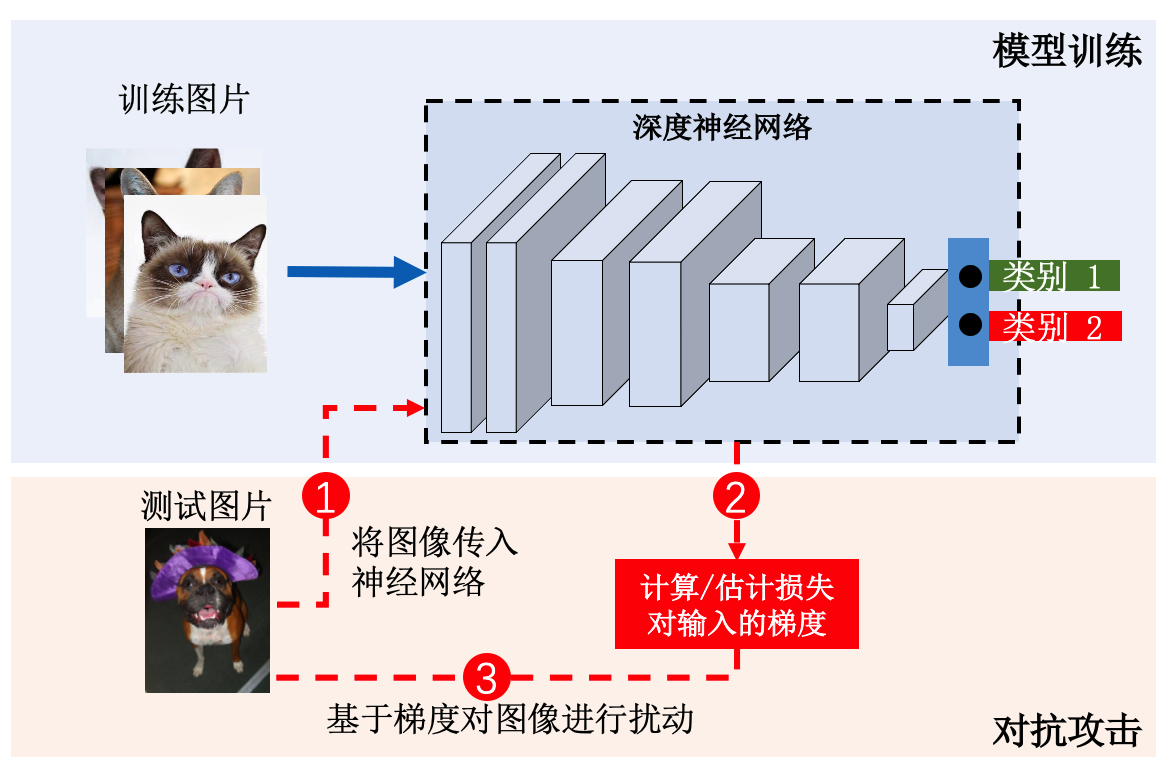
图3.1.1 模型训练（上半部分）与对抗攻击（下半部分）示意图¶

图3.1.1 展示了对抗攻击的一般流程及其与模型训练的三个主要区别。首先，对抗攻击发生在测试阶段，目标是一个已经训练好的模型，因此攻击样本是测试样本（如图中的测试图片）。其次，对抗攻击修改的是输入样本，而模型训练则调整模型参数。因此，对抗攻击需要计算或估计模型损失相对于输入的梯度信息。第三，对抗攻击通过梯度上升最大化模型的错误，而模型训练通过梯度下降最小化模型的错误。这些区别解释了对抗样本的设计思想，即在测试阶段通过修改输入样本来使模型出错。

根据攻击目标的不同，对抗攻击可以分为无目标攻击和有目标攻击。无目标攻击生成的对抗样本 \({\boldsymbol{x}}_{adv}\)会被目标模型（即被攻击的模型）错误分类为除真实类别之外的任意类别，即\(f({\boldsymbol{x}}_{adv}) \neq y\)；而有目标攻击生成的对抗样本\({\boldsymbol{x}}_{adv}\)则会被模型\(f\)错误预测为攻击者预设的目标类别\(y_{t}\)，即\(f({\boldsymbol{x}}_{adv}) = y_{t}\)且\(y_{t} \neq y\)。

根据攻击者能够获得的先验信息，对抗攻击还可以分为白盒攻击和黑盒攻击。白盒攻击假设攻击者可以获得目标模型的全部信息，包括训练数据、超参数、激活函数、模型架构和参数等。黑盒攻击则假设攻击者只能获得目标模型的输出信息（如预测值或概率），无法获得其他模型信息。相比之下，黑盒攻击更贴合实际应用场景，且具有更高的挑战性。接下来将介绍几种经典的白盒攻击和黑盒攻击方法。

3.1.1. 白盒攻击¶

在白盒设置下，给定目标模型 \(f\)和干净样本\({\boldsymbol{x}}\)（真实类别为\(y\)），有目标对抗攻击实际上是求解以下约束优化问题：

(3.1.1)¶\[\begin{split}\begin{aligned}& \min\ \|{\boldsymbol{x}}_{adv} - {\boldsymbol{x}}\|_{2} \\& \text{s.t.} \; f({\boldsymbol{x}}_{adv}) = y_{t}, \; {\boldsymbol{x}}_{adv} \in [0, 1]^{d}\end{aligned}\end{split}\]

其中，\(y_{t} \neq y\)为攻击者指定的目标类别，\({\boldsymbol{x}}_{adv}\)是样本\({\boldsymbol{x}}\)的对抗样本，\(d\)为输入样本的维度，\(\|\cdot\|_{2}\)表示\(L_2\) 范数。

L-BFGS攻击 上述优化问题难以精确求解，可以使用边界约束的L-BFGS（Limited-memory Broyden–Fletcher–Goldfarb–Shanno）算法来近似求解：

(3.1.2)¶\[\begin{split}\begin{aligned}& \min\ c{\lVert {\boldsymbol{x}}_{adv}-{\boldsymbol{x}} \rVert}_{2}+\mathcal{L}(f({\boldsymbol{x}}_{adv}), y_{t}) \\& \text{s.t.} \; {\boldsymbol{x}}_{adv} \in {[0, 1]}^{d}\end{aligned}\end{split}\]

其中，\(\mathcal{L}\)表示分类损失函数，如常用的交叉熵损失函数（cross-entropy）。基于上式，可以通过线性搜索得到\(c > 0\)的最小值，在此情况下，优化问题 (3.1.2) 的极小值也会满足\(f({\boldsymbol{x}}_{adv}) = y_{t}\)。通过L-BFGS攻击方法生成的对抗样本不但能攻击目标模型，还可以在不同模型和数据集之间迁移，即基于目标模型生成的对抗样本对其他使用不同超参数或者在不同子集上训练的模型也有攻击效果，但是攻击成功率会有所下降。

FGSM攻击 L-BFGS攻击方法生成对抗样本的效率比较低，需要对每个干净样本求解式 (3.1.2) ，所以用来评估模型的对抗鲁棒性时面临效率低的问题。我们可以基于损失函数的一阶梯度近似来设计更高效的攻击方法。快速梯度符号方法（Fast Gradient Sign Method, FGSM） (Goodfellow et al., 2015) 就是这样的一个攻击方法，其假设损失函数\(\mathcal{L}\)在样本\({\boldsymbol{x}}\)周围是线性的，即可以通过\({\boldsymbol{x}}\)处的一阶泰勒展开来近似。基于此，FGSM利用输入梯度（分类损失对输入求梯度）的符号信息（即梯度方向）进行一步固定步长的梯度上升来完成攻击：

(3.1.3)¶\[{\boldsymbol{x}}_{adv} = {\boldsymbol{x}} + \epsilon\cdot \text{sign}(\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}), y))\]

其中，\(\nabla_{{\boldsymbol{x}}}\mathcal{L}\)是损失对输入的梯度，步长大小直接设定为扰动上限\(\epsilon\)。与L-BFGS攻击方法相比，FGSM更简单、更高效，然而攻击成功率比较低。正是由于其简单性和高效性，FGSM已经成为对抗攻击与防御领域最为广泛使用的攻击方法之一。

BIM攻击 上述两种攻击都假设攻击者可以直接将对抗样本输入到目标模型中。然而，在物理世界场景中，攻击者往往只能通过外部设备（如摄像机和传感器等）来“传递”对抗样本，即攻击者所呈现的对抗样本往往是受害者通过外接设备捕获到的，而不是直接传入到模型中。为了使对抗样本在物理世界中保持对抗性，我们可以通过多步迭代的方式来不断调整攻击方向，提升其攻击性。这种攻击方法称为基本迭代方法（Basic Iterative Method，BIM） (Kurakin et al., 2018) ，其以更小的步长多次应用FGSM，并在每次迭代后对生成的对抗样本的像素值进行裁剪，以保证每个像素的变化都足够小。BIM攻击的迭代生成公式如下：

(3.1.4)¶\[\begin{split}\begin{aligned}{\boldsymbol{x}}_{adv}^{0} & = {\boldsymbol{x}} \\{\boldsymbol{x}}_{adv}^{t+1} & = \text{Clip}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t} + \alpha\cdot \text{sign}(\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}_{adv}^{t}), y))\}\end{aligned}\end{split}\]

其中，\(\text{Clip}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}^\prime\}=\min\{255,{\boldsymbol{x}}+\epsilon,\max\{0,{\boldsymbol{x}}−\epsilon,{\boldsymbol{x}}^\prime\}\}\)为裁剪操作，确保\({\boldsymbol{x}}\)的值在\([0,255]\)之间且对抗扰动大小不超过\(\epsilon\)，总迭代次数\(T\)设置为\(\min(\epsilon+4,1.25\epsilon)\)（像素取值范围为\([0,255]\)），步长为\(\alpha=\epsilon/T\)（\(T\)步迭代后正好达到\(\epsilon\)大小）。

PGD攻击 BIM攻击存在在规定步数内走不到\(\epsilon\)大小的情况，比如中间几步的梯度方向发生了翻转，这会导致对\(\epsilon\)空间探索不充分。这个问题可以通过使用投影梯度下降（Projected Gradient Descent，PGD） (Madry et al., 2018) 算法来有效解决。PGD攻击允许以更大的步长进行迭代生成，过程中如果生成的对抗样本超出了\(\epsilon\)空间则使用投影操作将其投回\(\epsilon\)球面。PGD攻击通过下面的公式迭代生成对抗样本：

(3.1.5)¶\[\begin{split}\begin{aligned}{\boldsymbol{x}}_{adv}^{0} & = {\boldsymbol{x}} + \boldsymbol{\zeta} \\{\boldsymbol{x}}_{adv}^{t+1} & = \text{Proj}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t} + \alpha\cdot \text{sign}(\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}_{adv}^{t}), y))\}\end{aligned}\end{split}\]

其中，\(\boldsymbol{\zeta}\)是从均匀分布\({\mathcal{U}}(-\epsilon,\epsilon)^{d}\)中采样得到的随机噪声，\(\text{Proj}_{{\boldsymbol{x}},\epsilon}\{\cdot\}\)是投影操作。另一个与BIM不同的地方在于，PGD攻击有一个随机初始化操作（即\({\boldsymbol{x}}_{adv}^{0} = {\boldsymbol{x}} + \boldsymbol{\zeta}\)），从干净样本的周围随机采样一个起始点来生成对抗样本，这可以帮助攻击跳出局部最优解。

FGSM和BIM通过最大化损失函数实现了无目标攻击，可以进一步通过最大化目标类别\(y_{t}\)的概率扩展到有目标攻击—FGSM有目标攻击和迭代最不可能类别攻击（Iterative Least Likely Class，ILLC）方法。基于FGSM的有目标攻击方法如下：

(3.1.6)¶\[{\boldsymbol{x}}_{adv} = {\boldsymbol{x}} - \epsilon\cdot \text{sign}(\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}), y_{t}))\]

当使用干净样本的最不可能类别\(y_{\text{LL}}=\mathop{\mathrm{arg\,min}}_{y}\{p(y|{\boldsymbol{x}})\}\)作为目标类别时，FGSM有目标攻击方法可被看作是单步的ILLC方法。基于多步扰动的ILLC攻击方法定义如下：

(3.1.7)¶\[\begin{split}\begin{aligned}{\boldsymbol{x}}_{adv}^{0} & = {\boldsymbol{x}} \\{\boldsymbol{x}}_{adv}^{t+1} & = \text{Clip}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t} - \alpha\cdot \text{sign}(\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}_{adv}^{t}), y_{\text{LL}}))\}\end{aligned}\end{split}\]

MI-FGSM攻击 虽然BIM比FGSM攻击性更强，但其在每次迭代时都会沿梯度方向“贪婪地”移动对抗样本，这容易导致过拟合于当前模型，陷入糟糕的局部最优解。这也会导致生成的对抗样本缺乏跨模型迁移能力。为了获得稳定的扰动方向并帮助对抗样本在迭代中摆脱局部最优解，后续研究将动量结合到BIM算法中，提出了动量迭代快速梯度符号方法（Momentum Iterative FGSM，MI-FGSM） (Dong et al., 2018) 。MI-FGSM生成对抗样本的公式如下：

(3.1.8)¶\[\begin{split}\begin{aligned}{\boldsymbol{g}}_{0} & = 0,\ {\boldsymbol{x}}_{adv}^{0} = {\boldsymbol{x}} \\{\boldsymbol{g}}_{t+1} & = \mu\cdot{\boldsymbol{g}}_{t} + \frac{\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}_{adv}^{t}), y))}{{\lVert \nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}_{adv}^{t}), y)) \rVert}_{1}} \\{\boldsymbol{x}}_{adv}^{t+1} & = \text{Clip}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t} + \alpha\cdot \text{sign}({\boldsymbol{g}}_{t+1})\}\end{aligned}\end{split}\]

其中，\({\boldsymbol{g}}_{t}\)为之前\(t\)次迭代的累积梯度，\(\mu\)是动量项的衰减因子。由于每次迭代中梯度的大小是不同的，所以每次迭代的梯度被其自身的\(L_1\)范数归一化。当\(\mu\)等于0时，MI-FGSM攻击算法就退化成了BIM攻击算法。

JSMA攻击 大多数对抗攻击都是对整个输入样本（比如整张图片）进行扰动，同时通过限制对抗噪声的\(L_{2}\)或\(L_{\infty}\)范数来保证隐蔽性。相比扰动全图来说，还有一类攻击方法追求的是扰动最少的像素来达到同样的攻击效果，它们统称为稀疏攻击方法。基于雅可比显著图的攻击（Jacobian-based Saliency Map Attack, JSMA） (Papernot et al., 2016) 就是一个基于\(L_{0}\)范数的稀疏攻击算法。JSMA是一种贪心算法，在每次迭代时只挑选一个对模型输出影响最大的像素进行修改。具体来说，JSMA首先计算模型的对抗梯度矩阵（雅可比矩阵）：

(3.1.9)¶\[J({\boldsymbol{x}})=\frac{\partial p({\boldsymbol{x}})}{\partial {\boldsymbol{x}}}=[\frac{\partial p(j|{\boldsymbol{x}})}{\partial {\boldsymbol{x}}_{i}}]_{i\times j}\]

其中，\(p(j|{\boldsymbol{x}})\)表示模型将\({\boldsymbol{x}}\)预测为类别\(j\)的概率，\({\boldsymbol{x}}_{i}\)为输入图片的第\(i\)个像素。接着，JSMA使用对抗梯度计算一个显著图，该图包含每个像素对分类结果的影响大小：越大的值表明修改它将显著增加被分类为某目标类别\(j\)的概率。在显著图中，每个像素\(i\)的显著值定义为：

(3.1.10)¶\[\begin{split}S({\boldsymbol{x}},y_{t})[i]=\begin{cases}0 \quad \text{if}\ J_{iy_{t}}({\boldsymbol{x}}) < 0\ \text{or}\ \sum\limits_{j\neq y_{t}}J_{ij}({\boldsymbol{x}}) > 0 \\J_{iy_{t}}({\boldsymbol{x}})|\sum\limits_{j\neq y_{t}}J_{ij}({\boldsymbol{x}})| \quad \text{otherwise}\end{cases}\end{split}\]

其中，\(J_{ij}({\boldsymbol{x}})\)表示\(\frac{\partial p(j|{\boldsymbol{x}})}{\partial {\boldsymbol{x}}_{i}}\)，即像素\({\boldsymbol{x}}_{i}\)对类别\(j\)的影响。给定显著图，JSMA每次选择一个最重要的像素并修改它以增加目标类别的概率。重复这一过程，直到超过预先设定的像素修改个数或者攻击成功。然而，由于计算一次对抗梯度只更新一个像素，所以JSMA攻击非常耗时。

Deepfool攻击 另外一个有代表性的攻击方法是Deepfool (Moosavi-Dezfooli et al., 2016) ，其使用从干净样本到决策边界的最近距离作为对抗噪声。Deepfool假设神经网络是线性的，存在超平面来区分各个类别。基于这一假设，可以直接推导出这个简化问题的最优解。但深度神经网络并不是线性的，所以在实际中仍需采用迭代的方式进行逐步求解。直观来说，改变线性分类器预测结果的最小噪声是从干净样本到仿射超平面\(\mathcal{F}=\{{\boldsymbol{x}}:{\boldsymbol{w}}^{\top}{\boldsymbol{x}}+b=0\}\)的距离。对于处在\({\boldsymbol{w}}^{\top}{\boldsymbol{x}}+b>0\)区域的干净样本来说，最小对抗噪声的形式为\(-\frac{{\boldsymbol{w}}^{\top}{\boldsymbol{x}}+b}{{\|{\boldsymbol{w}}\|}^{2}}{\boldsymbol{w}}\)。对于一般的可微二元分类器\(f\)，则可以采取迭代的方式，在每次迭代中假设\(f\)在\({\boldsymbol{x}}_i\)周围是线性的，线性分类器的最小对抗噪声为：

(3.1.11)¶\[\begin{split}\begin{aligned}& \mathop{\mathrm{arg\,min}}_{\boldsymbol{\eta}_{i}}{\|\boldsymbol{\eta}_{i}\|}_{2} \\& \text{s.t.} \; f({\boldsymbol{x}}_{i})+\nabla({\boldsymbol{x}}_{i})^{\top}\boldsymbol{\eta}_{i}=0\end{aligned}\end{split}\]

其中，第\(i\)次迭代计算得到的噪声\(\boldsymbol{\eta}_{i}\)会被用来更新\({\boldsymbol{x}}_{i}\)：\({\boldsymbol{x}}_{i+1}={\boldsymbol{x}}_{i}+\boldsymbol{\eta}_{i}\)。当\({\boldsymbol{x}}_{i}\)改变了分类器的预测类别时，迭代终止。最终的对抗噪声可以由多次迭代得到的累积噪声来近似。通过找到距离最近的超平面，Deepfool也可以扩展到攻击一般的多元分类器。与前面介绍的几个攻击方法相比，Deepfool可以生成与干净样本最接近的对抗样本。

CW攻击 这是由Carlini和Wagner在2017年提出的一种攻击方法 (Carlini and Wagner, 2017) ，CW的简写取自两个作者姓氏的首字母。CW攻击将噪声大小约束直接放到优化目标里进行优化（最小化），通过求解以下优化问题来生成对抗样本：

(3.1.12)¶\[\begin{split}\begin{aligned}& \min \ {\|{\boldsymbol{x}}_{adv}-{\boldsymbol{x}}\|}_{p}+c\cdot g({\boldsymbol{x}}_{adv}) \\& \text{s.t.} \;{\boldsymbol{x}}_{adv} \in {[0,1]}^d\end{aligned}\end{split}\]

其中，对抗目标函数\(g\)满足\(g({\boldsymbol{x}}_{adv})\leq 0\)当且仅当\(f({\boldsymbol{x}}_{adv})= y_t\)。\(g\)可以有不同的选择，其中实验验证最好的是下面的函数：

(3.1.13)¶\[g({\boldsymbol{x}}^\prime)=\max({\boldsymbol{z}}_{max}-{\boldsymbol{z}}_{y_{t}},-\kappa)\]

其中，\({\boldsymbol{z}}\)是模型的逻辑输出（logits），\({\boldsymbol{z}}_{max}=\max\left\{{\boldsymbol{z}}{({\boldsymbol{x}}^\prime)}_i:i\neq y_{t}\right\}\)表示错误类别中逻辑值最大的那个，参数\(\kappa\)为置信度超参，定义了目标类别\(y_t\)与其他类别间“应该具有”的最小逻辑值差异（即\({\boldsymbol{z}}_{max}\)至少要比\({\boldsymbol{z}}_{y_{t}}\)大\(\kappa\)）。与L-BFGS攻击方法不同，CW攻击引入了一个新的变量\(\boldsymbol{\omega}\in{\mathbb{R}}^{d}\)来避免边界约束，其中\(\boldsymbol{\omega}\)满足\({\boldsymbol{x}}_{adv}=\frac12(\tanh(\boldsymbol{\omega})+1)\)。通过巧妙的变量替换，将优化\({\boldsymbol{x}}_{adv}\)的边界约束最小化问题变成了优化\(\boldsymbol{\omega}\)的无约束最小化问题。

CW攻击有三个版本：\(L_{0}\)范数CW攻击（CW\(_0\)）、\(L_{2}\)范数CW攻击（CW\(_2\)）和\(L_{\infty}\)范数CW攻击（CW\(_{\infty}\)）。CW\(_2\)攻击求解以下优化问题：

(3.1.14)¶\[\begin{aligned}\min \ \|\frac12(\tanh(\boldsymbol{\omega})+1)-{\boldsymbol{x}}\|_2+c\cdot g(\frac12(\tanh(\boldsymbol{\omega})+1))\end{aligned}\]

由于\(L_{0}\)范数是不可微的，因此CW\(_0\)攻击采取迭代的方式，在每次迭代中确定一些对模型输出影响不大的像素，然后固定这些像素值不变，直到修改剩下的像素也无法再生成对抗样本。而像素的重要性是由CW\(_2\)攻击决定的。由于\(L_{\infty}\)范数不是完全可微的，因此CW\(_{\infty}\)攻击也采用了迭代的攻击方式，将目标函数中的\(L_{\infty}\)项替换为新的惩罚项：

(3.1.15)¶\[\min \ \sum\limits_i[(\boldsymbol{\eta}_i-\tau)^+]+c\cdot g({\boldsymbol{x}}+\boldsymbol{\eta})\]

每次迭代后，如果对于所有的\(i\)都有\(\boldsymbol{\eta}_i<\tau\)，则将\(\tau\)减少到原来的0.9倍，否则终止迭代。 CW攻击算法攻破了许多曾被认为是有效的防御策略，然而其生成对抗样本的计算开销很大，执行起来非常耗时。

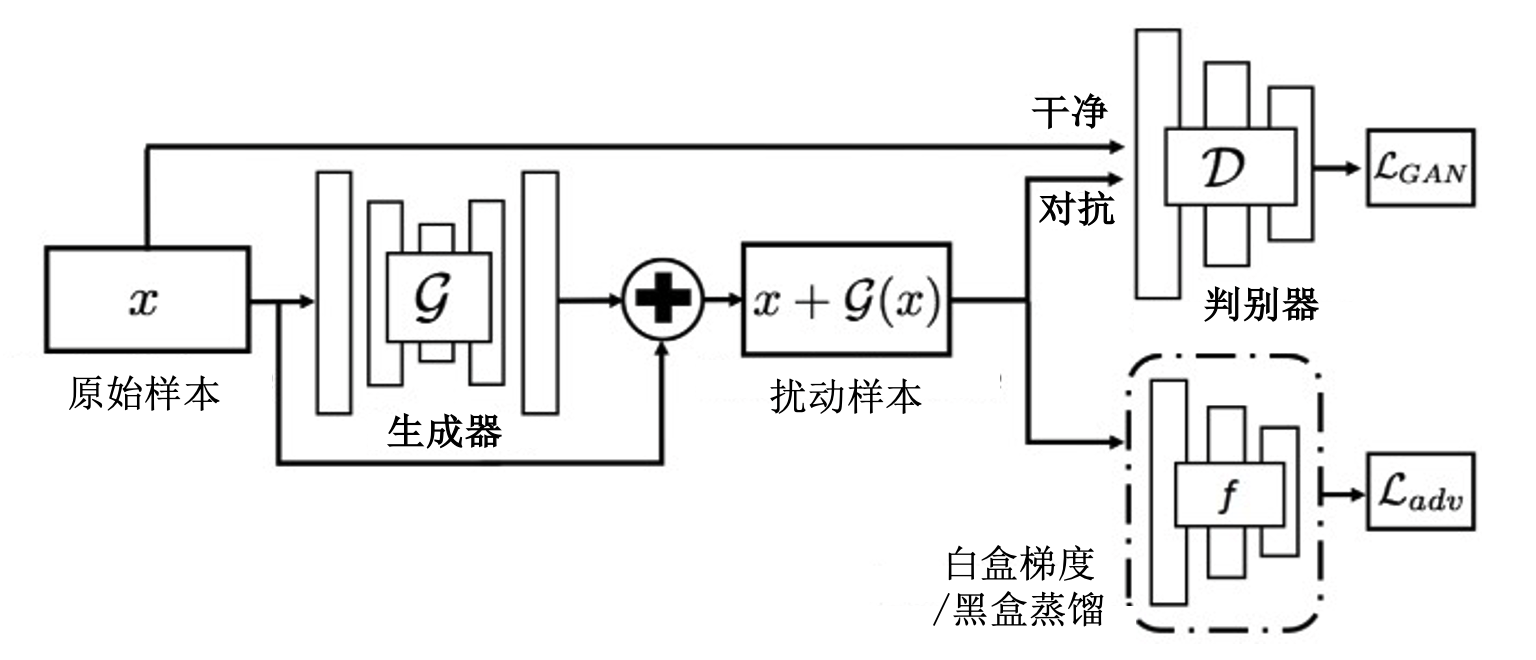
图3.1.2 AdvGAN方法示意图 (Xiao et al., 2018)¶

AdvGAN攻击 上面介绍的白盒攻击方法在生成每个对抗样本时都需要对目标模型进行访问，重复地进行扰动优化。为了避免每次都要优化，我们可以利用生成对抗网络提前学习对抗噪声的分布，之后给定任意一个干净样本都可以直接生成其所需要的对抗噪声。生成式的AdvGAN (Xiao et al., 2018) 攻击就是基于此思想提出来的，其通过训练一个生成器来学习干净样本的分布，并生成高度逼近干净分布的对抗噪声。如图3.1.2 所示，AdvGAN方法中的生成器\(\mathcal{G}\)将干净样本\({\boldsymbol{x}}\)作为输入，并生成一个噪声\(\mathcal{G}({\boldsymbol{x}})\)。添加了噪声的样本\({\boldsymbol{x}}+\mathcal{G}({\boldsymbol{x}})\)随后被输入到判别器\({\mathcal{D}}\)，判别器\({\mathcal{D}}\)会对其与原始干净样本\({\boldsymbol{x}}\)进行区分。其使用的GAN损失\(\mathcal{L}_{GAN}\)定义如下：

(3.1.16)¶\[\mathcal{L}_{GAN} = \mathbb{E}_{{\boldsymbol{x}} \sim D}\log({\mathcal{D}}({\boldsymbol{x}})) + \mathbb{E}_{{\boldsymbol{x}} \sim D}\log(1 - {\mathcal{D}}({\boldsymbol{x}} + \mathcal{G}({\boldsymbol{x}})))\]

为了实现针对目标模型\(f\)的白盒攻击，添加噪声的样本\({\boldsymbol{x}}+\mathcal{G}({\boldsymbol{x}})\)也会被输入到目标模型\(f\)，并输出损失\(\mathcal{L}_{adv}\)。在有目标攻击中，损失\(\mathcal{L}_{adv}\)会鼓励添加噪声的样本\({\boldsymbol{x}}+\mathcal{G}({\boldsymbol{x}})\)被目标模型\(f\)误分类为目标类别\(y_{t}\)：

(3.1.17)¶\[\mathcal{L}_{adv} = \mathbb{E}_{{\boldsymbol{x}} \sim D}\mathcal{L}(f({\boldsymbol{x}} + \mathcal{G}({\boldsymbol{x}})), y_{t})\]

为了限制噪声的大小，AdvGAN增加了一个基于\(L_{2}\)范数的铰链损失（hinge loss）：

(3.1.18)¶\[\mathcal{L}_{hinge} = \mathbb{E}_{{\boldsymbol{x}} \sim D}\max(0, \|\mathcal{G}({\boldsymbol{x}})\|_2 - \epsilon)\]

这也可以稳定GAN的训练。总体目标函数定义如下：

(3.1.19)¶\[\mathcal{L} = \mathcal{L}_{adv} + \alpha\mathcal{L}_{GAN} + \beta\mathcal{L}_{hinge}\]

其中，\(\alpha\)和\(\beta\)控制了每个损失项的重要程度。可以通过求解最小最大（min-max）化问题\(\mathop{\mathrm{arg\,min}}_\mathcal{G}\max_{\mathcal{D}}\mathcal{L}\)来训练\(\mathcal{G}\)和\({\mathcal{D}}\)。一旦\(\mathcal{G}\)在训练数据和目标模型上被训练，它可以给任意输入样本生成对抗噪声，且不再需要重复访问目标模型。除此之外，AdvGAN方法还可以被用于黑盒攻击，通过查询目标模型的输出，动态地训练蒸馏模型。在攻击对抗训练过的鲁棒模型时，AdvGAN取得了比FGSM和CW方法更高的攻击成功率。

AutoAttack攻击 虽然我们已经有各种攻击算法来评测一个模型的对抗鲁棒性，但是由于超参数调整不当、梯度遮掩（gradient masking）等陷阱，导致一些模型的鲁棒性仍会被高估，尤其是那些通过非常规手段训练的鲁棒模型。AutoAttack (Croce and Hein, 2020) 攻击通过自动调参策略来应对这个问题，有效避免了手动调参所带来的各种问题。AutoAttack集成了四种攻击算法，其中包括两个PGD的改进方法，即APGD-CE和APGD-DLR，这两个攻击方法是新提出的自动PGD（Auto-PGD）攻击方法的两个变体（损失函数不同）。具体来说，Auto-PGD在PGD的基础上添加了动量项：

(3.1.20)¶\[\begin{split}\begin{aligned}{\boldsymbol{z}}^{t+1} & = \text{Proj}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t} + \eta^{t}\cdot \text{sign}(\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}_{adv}^{t}), y))\} \\{\boldsymbol{x}}_{adv}^{t+1} & = \text{Proj}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t}+\alpha\cdot({\boldsymbol{z}}^{t+1}-{\boldsymbol{x}}_{adv}^{t})+(1-\alpha)\cdot({\boldsymbol{x}}_{adv}^{t}-{\boldsymbol{x}}_{adv}^{t-1})\}\end{aligned}\end{split}\]

其中，\(\eta^{t}\)是第\(t\)次迭代时的步长，\(\alpha\in[0,1]\)调节前一步更新对当前更新的影响。

Auto-PGD不需要选择步长并可以使用不同的损失函数，除迭代次数之外的其他参数都可以自动调整，可以克服PGD攻击由于固定步长和损失函数（交叉熵）所导致的评估不准确问题。此外，AutoAttack将两个PGD变体与两个现有的互补攻击—白盒快速自适应边界攻击（Fast Adaptive Boundary，FAB） (Croce and Hein, 2020) 和黑盒方形攻击（Square attack，Square） (Andriushchenko et al., 2020) 结合起来，组成了最终的集成攻击。FAB攻击旨在寻找改变给定输入类别所需的最小噪声，且对梯度遮掩鲁棒。Square攻击是一种基于分数的黑盒攻击，它使用随机搜索（而不是梯度近似）进行攻击，因此也不受梯度遮掩的影响。Square攻击在查询效率和成功率方面优于其他黑盒攻击，有时甚至与白盒攻击效果相当。这几种攻击方法的参数都不多，在不同的模型和数据集上具有很好的通用性，因此AutoAttack不需要特意调整任何参数。AutoAttack取得了更可靠的对抗鲁棒性评估结果，自2020年提出以来，已经被很多研究工作证明是迄今为止最强的攻击之一。

3.1.2. 黑盒攻击¶

黑盒攻击假设攻击者无法获得目标模型的参数信息以及其他细节，因此无法直接计算对抗梯度，只能通过估计梯度来生成对抗样本。对抗梯度可以通过零阶优化方法估计，也可以通过替代模型来近似。根据估计方式的不同，黑盒攻击可以分为查询攻击和迁移攻击。

3.1.2.1. 查询攻击¶

查询攻击（query-based attacks）通过查询目标模型获得模型输出，然后使用零阶优化方法来估计对抗梯度来生成对抗样本。虽然估计的梯度会存在一定误差，但是足以生成高成功率的对抗样本。根据目标模型输出类型的不同，查询攻击又可以分为基于分数的攻击和基于决策的攻击。基于分数的攻击需要模型输出完整的概率向量，而基于决策的攻击只需要模型输出类别标签。

基于分数的攻击：零阶优化（Zeroth Order Optimization，ZOO） (Chen et al., 2017) 攻击就是一种基于分数的黑盒攻击算法，其使用有限差分（finite difference）来估计目标模型的梯度。在CW攻击的基础上，ZOO攻击提出了一个新的基于模型预测概率的目标函数：

(3.1.21)¶\[g({\boldsymbol{x}}^\prime) = \max\{\max\limits_{i\neq y_{t}}\log[p(i|{\boldsymbol{x}})]-\log[p(y_{t}|{\boldsymbol{x}})], -\kappa\}\]

然后使用对称差商来估计梯度：

(3.1.22)¶\[\hat{{\boldsymbol{g}}}_{i} := \frac{\partial g({\boldsymbol{x}})}{\partial {\boldsymbol{x}}_{i}} \approx \frac{g({\boldsymbol{x}}+h{\boldsymbol{e}}_{i})-g({\boldsymbol{x}}-h{\boldsymbol{e}}_{i})}{2h}\]

其中，\(h\)是一个较小的常数，\({\boldsymbol{e}}_{i}\)是第\(i\)个分量为1的标准基向量。再进行一次梯度估计后可以得到二阶偏导（即Hessian矩阵）的估计：

(3.1.23)¶\[\hat{{\boldsymbol{h}}}_{i} := \frac{\partial^{2} g({\boldsymbol{x}})}{\partial {\boldsymbol{x}}_{ii}^{2}} \approx \frac{g({\boldsymbol{x}}+h{\boldsymbol{e}}_{i})-2g({\boldsymbol{x}})+g({\boldsymbol{x}}-h{\boldsymbol{e}}_{i})}{h^{2}}\]

上述方法的主要瓶颈是效率问题。如果估计所有坐标（\(d\)维）的梯度，总共需要计算\(2d\)次目标函数的值，而且有时可能需要经过数百次的迭代梯度下降才能让目标函数收敛。所以当干净样本维度很高时，这种方法可能会非常缓慢。为了解决这一问题，ZOO攻击算法使用了随机坐标下降方法，每次迭代时随机选择一个或一小批坐标进行梯度估计和更新，而且优先更新重要的像素可以进一步提高效率。为了加快计算时间和减少对目标模型的查询次数，ZOO还使用了攻击空间降维和分层攻击技术，将干净样本变换到更低的维度来生成对抗样本。虽然ZOO获得了与白盒CW攻击相当的性能，但由于坐标梯度估计方法不可避免地会对目标模型进行过多的查询，导致较低的查询效率。

AutoZOOM攻击 (Tu et al., 2019) 采用基于自动编码器的零阶优化方法（Autoencoder-based Zeroth Order Optimization）来进一步降低ZOO的查询复杂度。AutoZOOM构建了两个全新的模块：一个自适应的随机梯度估计策略，可以平衡查询次数和噪声大小，以及一个在其他未标记数据上离线训练好的自动编码器，或者是一个简单的双线性大小调整操作来加速攻击。为了提高查询效率，AutoZOOM放弃了坐标梯度估计，而是提出了缩放随机全梯度估计：

(3.1.24)¶\[{\boldsymbol{g}} = b\cdot\frac{g({\boldsymbol{x}}+\beta{\boldsymbol{u}})-g({\boldsymbol{x}})}{\beta}\cdot{\boldsymbol{u}}\]

其中，\(\beta > 0\)是平滑参数，\({\boldsymbol{u}}\)是从单位半径的欧几里得球体（Euclidean Ball）中随机均匀采样的单位长度向量，\(b\)是平衡梯度估计误差的偏差和方差的可调缩放参数。为了更有效地控制梯度估计的误差，AutoZOOM使用了平均随机梯度估计，计算在\(q\)个随机方向\(\{{{\boldsymbol{u}}_{j}}\}^{q}_{j=1}\)上的梯度估计的均值：

(3.1.25)¶\[\overline{{\boldsymbol{g}}} = \frac{1}{q}\sum_{j=1}^{q}{\boldsymbol{g}}_{j}\]

其中，\({\boldsymbol{g}}_{j}\)是式 (3.1.24) 中定义的梯度估计。 AutoZOOM通过自适应地调整\(q\)值来平衡查询次数和噪声大小。具体来说，首先将\(q\)设为1（使查询次数尽可能少），粗略地估计梯度以快速地完成初始攻击，然后设置\(q>1\)，更精确地估计梯度来微调图像质量，减小噪声。为了进一步提高查询效率和加速收敛，AutoZOOM从更小的维度\(d^\prime<d\)进行随机梯度估计。添加到干净样本上的对抗噪声实际上是在降维空间生成的，然后利用解码器\(D:{\mathbb{R}}^{d\prime}\mapsto{\mathbb{R}}^{d}\)从低维空间表示中重构出高维对抗噪声。AutoZOOM为解码器提供了两种选择：在不同于训练数据的未标记数据上离线训练的自动编码器或者双线性图像大小调整操作。与ZOO相比，AutoZOOM减少了平均查询的次数，同时保持了相当的攻击成功率。AutoZOOM还可以有效地微调图像质量，以保持与干净样本之间较高的视觉相似性。

NES攻击（系列） 除了有限差分和随机梯度估计之外，自然进化策略（Natural Evolutionary Strategies，NES）算法也可以用来估计对抗梯度，对应的黑盒攻击方法为NES (Ilyas et al., 2018) 。基于NES攻击，研究人员使用三种不同的威胁模型来模拟现实世界系统中访问受限和资源受限的情况。

威胁模型1：查询受限 此威胁模型限制了攻击者查询目标模型的次数。为了能在规定查询次数内完成攻击，可先基于NES算法来估计梯度，然后使用PGD算法和估计的梯度生成对抗样本。NES是一种基于搜索分布思想的无导数优化方法，最大化损失函数在搜索分布下的期望值而不是直接最大化损失函数。与有限差分方法相比，NES可以用更少的查询次数来估计梯度，具体如下:

(3.1.26)¶\[\mathbb{E}_{\pi(\boldsymbol{\theta}|{\boldsymbol{x}})}[\mathcal{L}(f(\boldsymbol{\theta}), y)] = \int \mathcal{L}(f(\boldsymbol{\theta}), y)\pi(\boldsymbol{\theta}|{\boldsymbol{x}})d\boldsymbol{\theta}\]

(3.1.27)¶\[\nabla_{{\boldsymbol{x}}}\mathbb{E}_{\pi(\boldsymbol{\theta}|{\boldsymbol{x}})}[\mathcal{L}(f(\boldsymbol{\theta}), y)] = \mathbb{E}_{\pi(\boldsymbol{\theta}|{\boldsymbol{x}})}[\mathcal{L}(f(\boldsymbol{\theta}), y)\nabla_{{\boldsymbol{x}}}\log(\pi(\boldsymbol{\theta}|{\boldsymbol{x}}))]\]

在当前样本\({\boldsymbol{x}}\)周围选择一个随机高斯噪声作为搜索分布，即\(\boldsymbol{\theta}={\boldsymbol{x}}+\sigma\boldsymbol{\delta},\ \boldsymbol{\delta}\sim{\mathcal{N}}(0,{\boldsymbol{I}})\)，并且使用通过对偶采样的\(n\)个\(\boldsymbol{\delta}_i\)来估计梯度：

(3.1.28)¶\[\nabla_{{\boldsymbol{x}}}\mathbb{E}_{\pi(\boldsymbol{\theta}|{\boldsymbol{x}})}[\mathcal{L}(f(\boldsymbol{\theta}), y)]\approx\frac{1}{\sigma n}\sum_{i=1}^{n}\boldsymbol{\delta}_{i}\mathcal{L}(f({\boldsymbol{x}}+\sigma\boldsymbol{\delta}_{i}), y)\]

最后，基于NES估计的梯度值，使用有动量项的PGD来生成对抗样本。一般来说，NES估计梯度的查询效率比有限差分方法快2-3个数量级。

威胁模型2：部分概率 此威胁模型限制攻击者只能获得前\(k\)个类别的概率或置信度分数。为了能在信息受限的情况下实现攻击，NES攻击没有从干净样本开始攻击，而是从属于目标类别的样本开始迭代优化，使用有动量项的PGD来生成对抗样本。在每次迭代时，需要交替进行下面两步：

在将目标类别样本投影到干净样本周围的过程中，需要将目标类别始终保持在前\(k\)个类别之中：

(3.1.29)¶\[\epsilon_n=\min\ \epsilon^\prime \quad \text{s.t.} \;\; \text{rank}(y_{t}|\text{Proj}_{\epsilon^\prime}({\boldsymbol{x}}_{adv}^{t-1}))<k\]
随着PGD的每次迭代更新，需要提高预测为目标类别的概率：

(3.1.30)¶\[{\boldsymbol{x}}_{adv}^t=\mathop{\mathrm{arg\,min}}_{{\boldsymbol{x}}^\prime}p(y_{t}|\text{Proj}_{\epsilon_{t-1}}({\boldsymbol{x}}^\prime))\]

威胁模型3：只有标签 此威胁模型限制攻击者无法获得类别的概率或置信度分数，只能获得一个按预测概率排序的\(k\)个类别标签的列表。为了能在仅获得类别标签的情况下实现攻击，NES攻击定义了对抗样本的离散分数\(R({\boldsymbol{x}}_{adv}^t)\)，仅基于目标类别标签\(y_{t}\)的排名变化，就可以量化每次迭代时输入样本的对抗程度：

(3.1.31)¶\[R({\boldsymbol{x}}_{adv}^t) = k-\text{rank}(y_{t}|{\boldsymbol{x}}_{adv}^t)\]

由于对抗样本对于随机噪声是鲁棒的，可以使用下面的离散分数替代类别概率来量化对抗程度：

(3.1.32)¶\[S({\boldsymbol{x}}_{adv}^t)=\mathbb{E}_{\boldsymbol{\delta}\sim {\mathcal{U}}[-\mu,\mu]}[R({\boldsymbol{x}}_{adv}^t+\boldsymbol{\delta})]\]

并使用蒙特卡洛近似估计该分数：

(3.1.33)¶\[\hat{S}({\boldsymbol{x}}_{adv}^t)=\frac{1}{N}\sum_{i=1}^{N}R({\boldsymbol{x}}_{adv}^t+\mu\boldsymbol{\delta}_{i})\]

用估计的\(\hat{S}({\boldsymbol{x}})\)来代替\(p(y_{t}|{\boldsymbol{x}})\)就可以满足第三种威胁模型，进而使用梯度\(\nabla_{{\boldsymbol{x}}}\hat{S}({\boldsymbol{x}})\)来生成对抗样本。

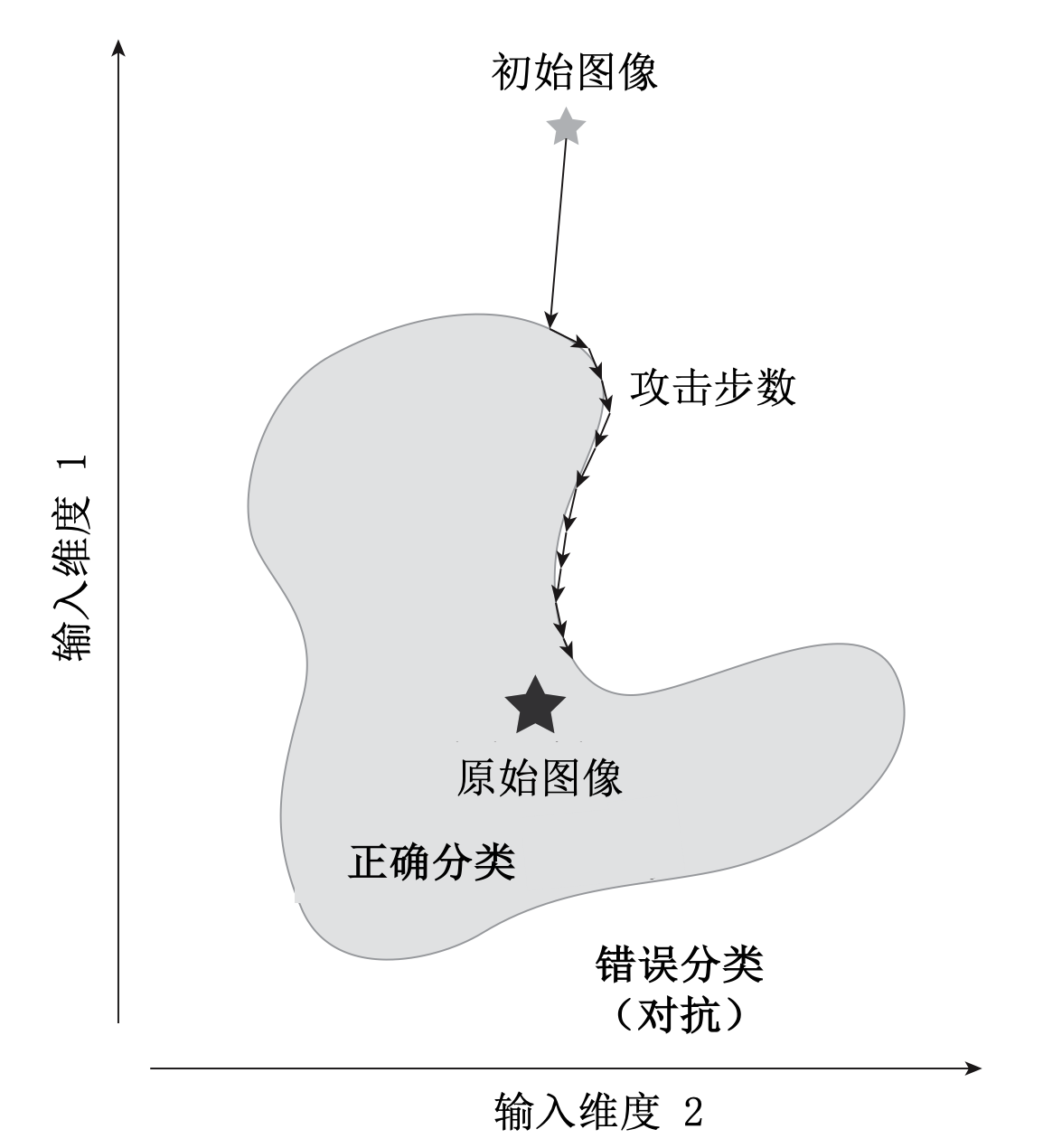
图3.1.3 边界攻击方法示意图 (Brendel et al., 2018)¶

基于决策的攻击：基于决策的攻击是上述第三种威胁模型在\(k=1\)时的特例，其中攻击者只能获得概率最高的类别标签。与基于分数的攻击相比，基于决策的攻击更加符合实际应用场景，因为在现实应用中攻击者很少能获得概率或置信度分数，同时目标模型也会使用梯度遮掩、内在随机性、对抗训练等防御策略进行鲁棒性增强。

边界攻击（Boundary Attack） (Brendel et al., 2018) 就是一个有代表性的基于决策的攻击算法。如图3.1.3 所示，边界攻击方法使用已经具有对抗性的样本进行初始化：a）在无目标攻击中，初始样本的每个像素从均匀分布\({\mathcal{U}}(0,255)\)中采样，并抛弃没有对抗性的初始样本；b）在有目标攻击中，初始样本为被预测成目标类别的样本。基于初始化样本，边界攻击沿着对抗区域和非对抗区域之间的决策边界游走，在每次迭代时都确保更新后的样本仍停留在对抗区域中，并且逐渐接近原始样本：

从高斯分布中采样得到噪声\(\boldsymbol{\eta}_{t}\sim{\mathcal{N}}(0,I)\)，然后重新缩放和裁剪样本，使其满足\({\boldsymbol{x}}_{adv}^{t-1}+\boldsymbol{\eta}_{t}\in[0,255]^d\)（保持有效像素值）和\(\|\boldsymbol{\eta}_{t}\|_2=\delta\cdot\|{\boldsymbol{x}}-{\boldsymbol{x}}_{adv}^{t-1}\|_2\)（约束扰动幅度）。
将\(\boldsymbol{\eta}_{n}\)投影到干净样本\({\boldsymbol{x}}\)周围的一个球面上得到正交噪声，使其满足\(\|{\boldsymbol{x}}-({\boldsymbol{x}}_{adv}^{t-1}+\boldsymbol{\eta}_{t})\|_2=\|{\boldsymbol{x}}-{\boldsymbol{x}}_{adv}^{t-1}\|_2\)。
向干净样本的方向移动一步，使其满足\(\|{\boldsymbol{x}}-{\boldsymbol{x}}_{adv}^{t-1}\|_2-\|{\boldsymbol{x}}-({\boldsymbol{x}}_{adv}^{t-1}+\boldsymbol{\eta}_{t})\|_2=\epsilon\cdot\|{\boldsymbol{x}}-{\boldsymbol{x}}_{adv}^{t-1}\|_2\)。

在攻击过程中，可以根据边界的局部几何形状来动态地调整\(\delta\)和\(\epsilon\)。边界攻击方法的基本运行原理非常简单，但它也需要大量的查询来探索高维空间，而且缺乏收敛保证。

基于优化的攻击（Optimization-based attack，Opt-attack） (Cheng et al., 2019) 将基于决策的攻击重新表示为一个实值优化问题。由于转换得到的实值优化问题通常是连续的，所以可以通过任何一个零阶优化方法来求解，从而提高查询效率。无目标Opt-attack攻击的对抗目标函数为：

(3.1.34)¶\[g(\boldsymbol{\theta}) = \min\limits_{\lambda>0}\lambda \quad \text{s.t.} \;f({\boldsymbol{x}}+\lambda \frac{\boldsymbol{\theta}}{\|\boldsymbol{\theta}\|})\neq y\]

相应地，有目标Opt-attack攻击的对抗目标函数为：

(3.1.35)¶\[g(\boldsymbol{\theta}) = \min\limits_{\lambda>0}\lambda \quad \text{s.t.} \;f({\boldsymbol{x}}+\lambda \frac{\boldsymbol{\theta}}{\|\boldsymbol{\theta}\|})=y_{t}\]

其中，\(\boldsymbol{\theta}\)表示搜索方向，\(g(\boldsymbol{\theta})\)是干净样本\({\boldsymbol{x}}\)沿方向\(\boldsymbol{\theta}\)到最近对抗样本的距离。对于归一化后的\(\boldsymbol{\theta}\)，Opt-attack使用粗粒度搜索和二分搜索来计算目标函数的值\(g(\boldsymbol{\theta})\)。Opt-attack方法并没有搜索对抗样本，而是搜索方向\(\boldsymbol{\theta}\)来最小化对抗噪声\(g(\boldsymbol{\theta})\)，那么就有了下面的优化问题：

(3.1.36)¶\[\min\limits_{\boldsymbol{\theta}}g(\boldsymbol{\theta})\]

为了求解上述优化问题，Opt-attack使用随机无梯度（Randomized Gradient-Free，RGF）方法来估计梯度：

(3.1.37)¶\[\hat{{\boldsymbol{g}}}=\frac{g(\boldsymbol{\theta}+\beta{\boldsymbol{u}})-g(\boldsymbol{\theta})}{\beta}\cdot{\boldsymbol{u}}\]

然后，以步长\(\alpha\)通过\(\boldsymbol{\theta}\leftarrow\boldsymbol{\theta}-\alpha\hat{{\boldsymbol{g}}}\)来更新搜索方向。最后，通过优化问题 (3.1.36) 的最优解\(\boldsymbol{\theta}^{*}\)得到对抗样本\({\boldsymbol{x}}_{adv}={\boldsymbol{x}}+g(\boldsymbol{\theta}^{*})\frac{\boldsymbol{\theta}^{*}}{\|\boldsymbol{\theta}^{*}\|}\)。当目标函数\(g(\boldsymbol{\theta})\)是Lipschitz平滑时，Opt-attack方法在查询次数上有收敛保证。此外，Opt-attack方法还可以攻击除深度神经网络以外的其他离散的、不可微的机器学习模型，例如梯度增强决策树（Gradient Boosting Decision Tree，GBDT）等。与边界攻击方法相比，Opt-attack方法将查询次数减少了3-4倍，实现了更小或类似的对抗噪声。

查询攻击通常可以取得较高的攻击成功率，但是它们也需要大量的查询才能攻击成功。借助一些先验知识可以进一步优化和加速此类攻击，此外，查询攻击还可以用代价更低的迁移攻击作为初始化来降低查询次数。

3.1.2.2. 迁移攻击¶

早在2013年，Szegedy等人 (Szegedy et al., 2014) 就发现了对抗样本的跨模型迁移性。由于不同的模型在相同数据点周围学到了有一定重叠的决策边界，使得基于一个模型生成的对抗样本往往也可以欺骗在相同数据集上（独立）训练的其他模型，尤其是结构相同或相似的模型。

迁移攻击便利用了对抗样本的迁移性来实现黑盒攻击。攻击者首先借助替代模型（surrogate model）并使用白盒攻击方法生成对抗样本，然后用生成的对抗样本来攻击目标模型。如此，攻击者可以自己训练替代模型，且替代模型不需要跟目标模型结构一样，仅需要替代模型的训练数据跟目标模型的训练数据来自于同一个分布。

近似模型攻击：好的替代模型可以让攻击事半功倍。可是什么样的替代模型才算是好的呢？研究发现，攻击者可以训练一个替代模型去主动逼近目标模型（类似模型抽取的思想） (Papernot et al., 2017) 。具体来说，攻击者可以先根据先验知识合成一些数据，然后将这些数据输入到目标模型得到它的输出，并将这些输出作为类别标签去训练替代模型。在这个过程中，攻击者还可以动态选择样本，使用更少的关键样本来训练替代模型。然而，这种攻击方法需要大量的查询并且需要目标模型输出全类别概率向量。这些要求在实际应用场景中很难满足，尤其是包含上千类的图像识别模型，其往往只返回部分预测类别信息。此外，直接使用白盒攻击方法在替代模型上生成的对抗样本的迁移性存在一定局限，往往还需要其他技术进行进一步增强。

集成模型攻击：另外一种迁移性提升策略是集成多个替代模型 (Liu et al., 2017) ，这样就可以避免对单个替代模型的过拟合。简单来说，如果一个对抗样本对多个模型都具有对抗性，那么它极有可能具有很好的迁移性。给定\(k\)个替代模型，基于模型集成的有目标迁移攻击求解以下优化问题：

(3.1.38)¶\[\mathop{\mathrm{arg\,min}}_{{\boldsymbol{x}}_{adv}} -\log(\sum_{i=1}^{k}\alpha_{i}p_{i}(y_{t}|{\boldsymbol{x}}_{adv}))+\lambda\|{\boldsymbol{x}}_{adv}-{\boldsymbol{x}}\|_2\]

其中，\(\alpha_{i}\)是给每个模型的权重（\(\alpha_{i}\geq0\)且\(\sum_{i=1}^{k}\alpha_{i}=1\)），\(p_{i}(y_{t}|\cdot)\)是第\(i\)个替代模型预测类别\(y_{t}\)的概率。无目标迁移攻击与式 (3.1.38) 类似，不过最大化的是模型对真实类别的分类错误。因为融合的是模型输出的概率向量，所以这是一种概率融合攻击方法。集成是一种通用的思想，其他现有的攻击方法，如MI-FGSM攻击见式 (3.1.8) ），也可以通过融合损失函数或者逻辑输出来集成多个替代模型：

(3.1.39)¶\[\sum_{i=1}^{k}\alpha_{i}\mathcal{L}(f({\boldsymbol{x}}_{adv}), y_{t})\]

(3.1.40)¶\[\sum_{i=1}^{k}\alpha_{i}{\boldsymbol{z}}_{i}({\boldsymbol{x}}_{adv})\]

上述两种融合方式产生了不同的攻击性能，实验表明融合逻辑输出（即式 (3.1.40) ）要优于融合预测概率和融合损失函数。

DI\(^2\)-FGSM攻击：有研究认为生成对抗样本与模型训练类似，而迁移性则对应模型泛化。基于模型集成的攻击方法和MI-FGSM也在某种程度上证明了这一观点，所以可以借鉴其他提升模型泛化的技术来提高迁移攻击的性能。\({\text{DI}}^2\)-FGSM (Xie et al., 2019) 攻击通过创建更多样化的输入模式来提高对抗样本的迁移性。 \({\text{DI}}^2\)-FGSM的攻击过程类似于BIM攻击，但是在每次迭代时以概率\(p\)对输入进行图像变换\(T(\cdot)\)，从而缓解对替代模型的过拟合：

(3.1.41)¶\[{\boldsymbol{x}}_{adv}^{t+1} = \text{Clip}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t}+ \alpha\cdot \text{sign}(\nabla_{{\boldsymbol{x}}}\mathcal{L}(f(T({\boldsymbol{x}}_{adv}^{t};p)),y))\}\]

其中，随机图像变换函数\(T({\boldsymbol{x}}_{adv}^{\top};p)\)定义为：

(3.1.42)¶\[\begin{split}T({\boldsymbol{x}}_{adv}^{\top};p)=\begin{cases}T({\boldsymbol{x}}_{adv}^{\top}) & \text{概率}\;p \\{\boldsymbol{x}}_{adv}^{\top} & \text{概率}\;1-p\end{cases}\end{split}\]

\({\text{DI}}^2\)-FGSM使用随机变换包括：随机大小调整（将输入图像调整为随机大小）、随机填充（随机在输入图像边缘填充零元素）等。随机变换函数中的随机变换概率\(p\)平衡了\({\text{DI}}^2\)-FGSM的白盒成功率和黑盒成功率。当\(p=0\)时，\({\text{DI}}^2\)-FGSM就退化为BIM攻击，从而导致生成的对抗样本过拟合替代模型；当\(p=1\)时，则只将随机变换后的输入图像用于对抗攻击，虽然这样可以显著提高生成对抗样本的黑盒成功率，但同时也会使得白盒成功率变差。虽然MI-FGSM和\({\text{DI}}^2\)-FGSM是两种完全不同的缓解过拟合的方法，但二者可以自然地组合起来形成更强的攻击，即动量多样化输入迭代快速梯度符号方法（Momentum Diverse Inputs Iterative FGSM, M-\({\text{DI}}^2\)-FGSM）。M-\({\text{DI}}^2\)-FGSM的整体攻击过程与MI-FGSM类似，只需将动量的计算替换为：

(3.1.43)¶\[{\boldsymbol{g}}_{t+1}=\mu\cdot{\boldsymbol{g}}_{t}+\frac{\nabla_{{\boldsymbol{x}}}\mathcal{L}(f(T({\boldsymbol{x}}_{adv}^{t};p)), y))}{\|\nabla_{{\boldsymbol{x}}}\mathcal{L}(f(T({\boldsymbol{x}}_{adv}^{t};p)),y))\|_{1}}\]

平移不变攻击：尽管MI-FGSM和\({\text{DI}}^2\)-FGSM生成的对抗样本在普通训练的模型上具有较高的迁移性，但它们却很难有效地迁移到鲁棒训练的模型。因为鲁棒模型用来识别物体类别的判别区域不同于普通训练的模型，MI-FGSM和\({\text{DI}}^2\)-FGSM生成的对抗样本与替代模型在给定干净样本上的判别区域相关，从而很难迁移到其他具有不同判别区域的目标模型。而这个问题可以由平移不变（translation invariant）技术来解决，让生成的对抗样本对替代模型的判别区域不敏感，且可以与已有攻击方法相结合，进一步提升迁移性。基于平移不变技术的攻击方法使用原始干净图像和平移后的干净图像所组成的图像集来生成对抗样本：

(3.1.44)¶\[\mathop{\mathrm{arg\,min}}_{{\boldsymbol{x}}_{adv}} \sum_{i,j}\omega_{ij}\mathcal{L}(f(T_{ij}({\boldsymbol{x}}_{adv})), y)\quad \text{s.t.} \; \|{\boldsymbol{x}}_{adv}-{\boldsymbol{x}}\|_{\infty}\leq\epsilon\]

其中，\(T_{ij}({\boldsymbol{x}})\)是将图像\({\boldsymbol{x}}\)沿两个维度方向分别平移\(i\)和\(j\)个像素的平移操作，平移后图像的每个像素\((a,b)\)为\(T_{ij}({\boldsymbol{x}})_{a,b}={\boldsymbol{x}}_{a−i,b−j}\)，\(\omega_{ij}\)是损失函数\(\mathcal{L}(f(T_{ij}({\boldsymbol{x}}_{adv})), y)\)的权重，\(i,j\in \{−k,\cdots,0,\cdots,k\}\)， \(k\)是要平移的最大像素数。通过这种方法生成的对抗样本对于替代模型的判别区域不太敏感，可以以更高的概率欺骗鲁棒模型。

然而，要生成上述对抗样本需要计算集合中所有图像的梯度，这会带来很大的计算开销。为了提高攻击效率，可以利用卷积神经网络中的平移不变性，即输入图像中的物体在很小的平移下也可以被正确识别。平移不变攻击可以通过将未平移样本的梯度与一个预定义的由所有权重\(\omega_{ij}\)组成的核矩阵进行卷积来实现。改进后的平移不变攻击可以在不增加计算复杂度的情况下，自然地与FGSM和BIM结合分别得到TI-FGSM和TI-BIM攻击方法：

(3.1.45)¶\[{\boldsymbol{x}}_{adv}={\boldsymbol{x}}+\epsilon\cdot \text{sign}({\boldsymbol{W}}*\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}),y))\]

(3.1.46)¶\[{\boldsymbol{x}}_{adv}^{t+1}=\text{Clip}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t}+\alpha\cdot \text{sign}({\boldsymbol{W}}*\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}_{adv}^{t}),y))\}\]

其中，\({\boldsymbol{W}}\)是大小为\((2k+1)\times(2k+1)\)的核矩阵，\({\boldsymbol{W}}_{i,j}=w_{−i−j}\)。设计核矩阵的基本原则是给平移较大的图像赋予相对较小的权重，这可以采用高斯核矩阵来实现。

在可结合的防过拟合技术方面，除了MI-FGSM之外，还可以考虑与Nesterov加速梯度（Nesterov Accelerated Gradient，NAG）结合得到Nesterov迭代快速梯度符号方法（Nesterov Iterative FGSM，NI-FGSM）。NAG可以看作是动量的改进。与动量相比，除了稳定更新方向之外，NAG的期望更新还可以为之前积累的梯度进行一次修正，这有助于有效地向前看。NAG的这种前瞻性可以帮助对抗样本更容易、更快速地摆脱糟糕的局部最优解，从而提高迁移性。NI-FGSM在每次迭代计算梯度之前，会先沿着之前积累的梯度方向进行一次跳跃：

(3.1.47)¶\[\begin{split}\begin{aligned}{\boldsymbol{x}}_{\text{ne}}^{t} & = {\boldsymbol{x}}_{adv}^{t} + \alpha\cdot\mu\cdot{\boldsymbol{g}}_{t} \\{\boldsymbol{g}}_{t+1} & = \mu\cdot{\boldsymbol{g}}_{t} + \frac{\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}_{\text{ne}}^{t}), y))}{\|\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}_{\text{ne}}^{t}), y))\|_{1}} \\{\boldsymbol{x}}_{adv}^{t+1} & = \text{Clip}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t} + \alpha\cdot \text{sign}({\boldsymbol{g}}_{t+1})\}\end{aligned}\end{split}\]

其中，\(\mu\)是\({\boldsymbol{g}}_{t}\)的衰减因子。NI-FGSM能够在梯度累积部分取代MI-FGSM，并产生更好的攻击性能。

在数据增强技术方面，除了平移不变性以外，深度神经网络还具有缩放不变性，即在同一模型上原图像和缩放后的图像的损失是相似的。利用模型的缩放不变特性，可以进一步提出缩放不变攻击（Scale-Invariant attack Method，SIM）。缩放不变攻击在缩放样本上优化对抗噪声：

(3.1.48)¶\[\mathop{\mathrm{arg\,min}}_{{\boldsymbol{x}}_{adv}}\frac{1}{m}\sum_{i=0}^{m}\mathcal{L}(f(S_{i}({\boldsymbol{x}}_{adv})), y)\quad \text{s.t.}\; \|{\boldsymbol{x}}_{adv}-{\boldsymbol{x}}\|_{\infty}\leq\epsilon\]

其中，\(S_{i}({\boldsymbol{x}})={\boldsymbol{x}}/2^{i}\)表示缩放系数为\(1/2^{i}\)的干净图像\({\boldsymbol{x}}\)的缩放副本，\(m\)表示缩放副本的数量。从形式上来看，缩放不变攻击和基于模型集成的攻击比较类似。不同的是，模型集成攻击需要训练一组不同的替代模型，这会带来更多的计算开销，而缩放不变攻击可以看作是以模型增强（一种通过保留损失变换获得多个模型的简单方法）的方式从原始模型中衍生出多个模型。

跳跃梯度攻击：尽管上述基于迁移的攻击方法都很有效，但它们都忽略了深度神经网络的结构特性。迁移性差的一个很重要的原因是替代模型与目标模型存在结构差异。为此，跳跃梯度攻击（Skip Gradient Method，SGM） (Wu et al., 2020) 利用残差神经网络中的跳连（skip connection）操作，通过在反向梯度传播过程中有选择性的跳过某些连接来模拟不同深度的神经网络，从而提高生成对抗样本的迁移性。在残差网络中，跳连使用恒等映射（identify mapping）将卷积模块的输入直接连接到其输出，以此来建立一个从浅层到深层的捷径（shortcut）\({\boldsymbol{z}}_{i+1}={\boldsymbol{z}}_{i}+f_{i+1}({\boldsymbol{z}}_{i})\)。具有\(L\)个残差模块的残差神经网络可以表示为：

(3.1.49)¶\[{\boldsymbol{z}}_{L} = {\boldsymbol{z}}_{0} + \sum_{i=0}^{L-1}f_{i+1}({\boldsymbol{z}}_{i})\]

其中，\({\boldsymbol{z}}_{0}={\boldsymbol{x}}\)是模型的输入。根据链式法则，损失函数\(\mathcal{L}(f({\boldsymbol{x}}),y))\)对于输入\({\boldsymbol{z}}_{0}\)的梯度可以分解为：

(3.1.50)¶\[\frac{\partial \mathcal{L}(f({\boldsymbol{x}}),y))}{\partial {\boldsymbol{x}}} = \frac{\partial \mathcal{L}(f({\boldsymbol{x}}),y))}{\partial {\boldsymbol{z}}_{L}}\prod_{i=0}^{L-1}(\frac{\partial f_{i+1}(\partial {\boldsymbol{z}}_{i})}{{\boldsymbol{z}}_{i}} + 1)\frac{\partial {\boldsymbol{z}}_{0}}{\partial {\boldsymbol{x}}}\]

为了使用更多来自跳跃连接的梯度，SGM攻击向分解梯度种引入了一个衰减参数，以减少来自卷积模块的梯度：

(3.1.51)¶\[\nabla_{{\boldsymbol{x}}}\mathcal{L}(f({\boldsymbol{x}}), y) = \frac{\partial \mathcal{L}(f({\boldsymbol{x}}),y))}{\partial {\boldsymbol{z}}_{L}}\prod_{i=0}^{L-1}(\gamma\frac{\partial f_{i+1}(\partial {\boldsymbol{z}}_{i})}{{\boldsymbol{z}}_{i}} + 1)\frac{\partial {\boldsymbol{z}}_{0}}{\partial {\boldsymbol{x}}}\]

其中，\(\gamma\in(0,1]\)是衰减参数。SGM算法可以在不增加任何计算开销的情况下，很容易地与基于梯度的攻击方法相结合。比如，与BIM结合，迭代地生成对抗样本：

(3.1.52)¶\[{\boldsymbol{x}}_{adv}^{t+1}=\text{Clip}_{{\boldsymbol{x}},\epsilon}\{{\boldsymbol{x}}_{adv}^{t}+\alpha\cdot \text{sign}(\frac{\partial \mathcal{L}(f({\boldsymbol{x}}),y))}{\partial {\boldsymbol{z}}_{L}}\prod_{i=0}^{L-1}(\gamma\frac{\partial f_{i+1}(\partial {\boldsymbol{z}}_{i})}{{\boldsymbol{z}}_{i}} + 1)\frac{\partial {\boldsymbol{z}}_{0}}{\partial {\boldsymbol{x}}})\}\]

卷积模块的梯度是沿着反向传播路径累积衰减的，也就是说，浅层卷积模块的梯度将比深层卷积模块的梯度减小更多倍。由于浅层特征已经被跳跃连接很好地保留了，卷积模块梯度的衰减则会鼓励攻击更多关注浅层特征，而浅层特征在不同的深度神经网络之间更容易迁移。但是，SGM只对有跳跃连接的神经网络结构适用，其在其他网络结构上的扩展值得进一步探索。

虽然上述迁移攻击方法都可以提升对抗样本的迁移性，但攻击成功率仍然不如查询攻击，因为毕竟缺失了来自目标模型的反馈。但是查询攻击又依赖模型的输出类型，且往往受查询次数限制，在现实场景中难以实施。二者的融合可以产生更高效的攻击方法。比如，可以尝试用基于替代模型生成的对抗噪声作为初始化，然后用查询攻击来进行微调，再结合一定的先验知识，相信可以让黑盒攻击变得和白盒攻击一样准确高效。

3.1.3. 物理攻击¶

前面介绍的黑盒攻击和白盒攻击算法都假定用于攻击的对抗样本可以在生成后原封不动地直接输入目标模型。而现实场景中的人工智能系统往往通过摄像头和传感器等设备获取输入，而无法直接接受纯数字输入。比如，在人脸识别场景中，用户的面部图像是通过摄像头采集的，而不是上传图像。在这些场景下，对输入样本进行细粒度（逐像素）修改的攻击方式就变得不切实际了，需要专门的物理世界攻击（physical-world attack）方法来实现它们在真实环境中的对抗性。

物理对抗样本 对样噪声的“人眼不可见”属性激发了研究者的兴趣，但是“这种人眼不可见的噪声是否真能存在于物理世界”？为了回答这个问题，研究人员通过“打印-重拍摄”的方式进行了系列物理实验 (Kurakin et al., 2018) 。如图3.1.4 所示，研究者们先使用传统的攻击算法（可以统称为“数字攻击”）生成一些对抗图片。之后，他们将原始图片和对抗图片打印出来，并重新拍摄成照片（使用谷歌手机Nexus 5X）。最后，将这些照片中所包含的图像分割出来，输入分类模型中进行测试。实验表明，一部分对抗样本在经过拍照后依然可以成功攻击。进一步实验发现，改变照片亮度和对比度对对抗样本影响不大，但是模糊、噪点和JPEG编码会在很大程度上破坏对抗样本的有效性。

../_images/6.4_robust_physical_attack.png

图3.1.4 物理世界攻击 (Kurakin et al., 2018)¶

鲁棒物理扰动 虽然上述工作证明了对抗样本在物理世界中也能发挥作用，但是实验中的物理攻击是将对抗样本打印后正对拍摄，这实际上与真实场景还存在一些差异。为此，后来的研究者做了更近一步的探索。实验选择道路标志牌作为检测和识别目标，并指出在物理世界中，对抗样本的有效性存在以下挑战：

环境条件：现实世界中拍摄的图片会有不同的距离、角度、光照和天气等因素。
空间限制：大部分攻击在整张图片上添加扰动，而现实情况是，攻击者无法对路牌以外的背景进行改变，并且背景也会随拍摄视角不同而发生变化。
扰动限制：很多攻击生成的对抗扰动过于微小，摄像头往往无法感知这些扰动，导致攻击容易失效。
制造误差：通过攻击算法计算出来的对抗噪声可能包含无法在现实世界中打印出来的颜色值。

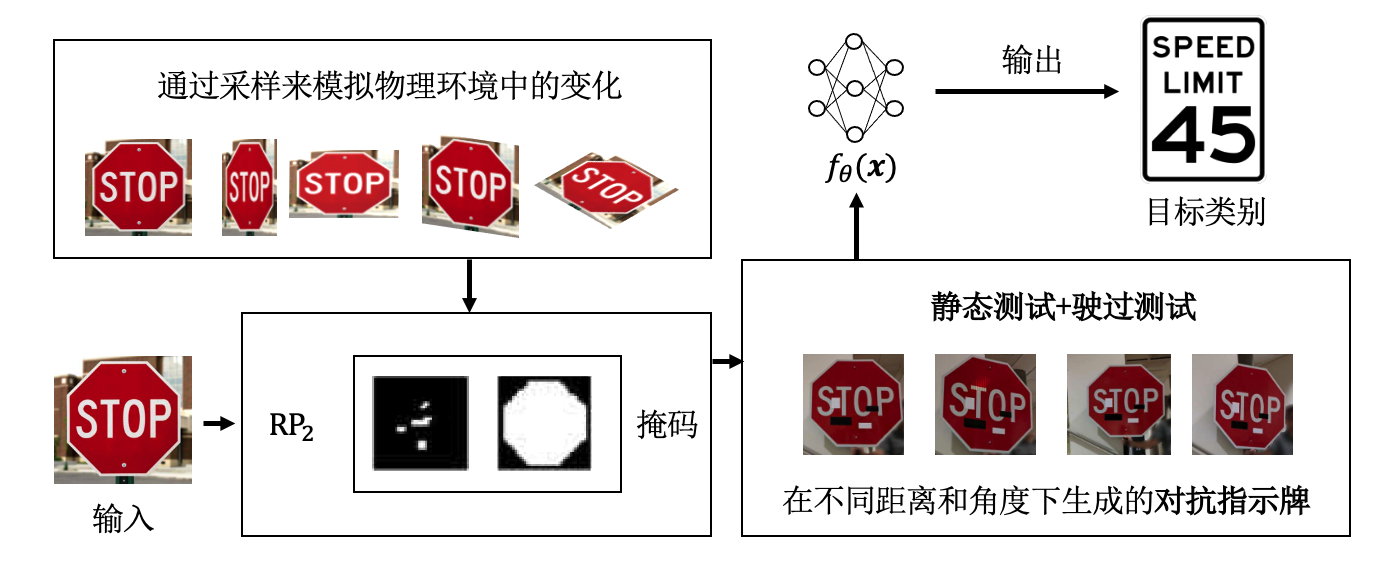
图3.1.5 RP\(_{2}\)的攻击流程 (Eykholt et al., 2018)¶

受以上挑战启发，研究人员提出鲁棒物理扰动（Robust Physical Perturbations，RP\(_{2}\)）攻击算法 (Eykholt et al., 2018) ，该算法可以产生一个可见但并不显眼的、只作用于目标物体而非环境的扰动，并且这个扰动对不同距离和角度的摄像头具有较高的鲁棒性。图3.1.5 展示了RP\(_{2}\)算法的攻击流程，其首先基于传统数字攻击算法生成对抗扰动：

(3.1.53)¶\[\underset{\boldsymbol{\delta}}{\mathop{\mathrm{arg\,min}}} \,\lambda\|\boldsymbol{\delta}\|_{p}+\mathcal{L}(f({\boldsymbol{x}}+\boldsymbol{\delta}), y_{t})\]

其中，\(y_{t}\)为目标类别。为了能够适应上述物理世界挑战中的环境条件，研究人员拍摄了在不同距离、角度及光线下的路牌照片来反映动态多变的物理环境。他们还通过合成手段，如随机裁切图片中的目标、改变亮度、添加空间变换等来模拟各种可能的情况。将这些不同条件下的物理变换和合成变换的分布建模成\(X^V\)，用于训练的实例\({\boldsymbol{x}}_i\)均从\(X^V\)中抽取。

为了保证扰动只添加在目标物体\(o\)上，RP\(_{2}\)使用输入掩码（input mask）来将计算出的扰动添加到物理目标区域内。该输入掩码为一个矩阵\(M_{{\boldsymbol{x}}}\)，维度与输入图片大小相同，在没有添加扰动的区域掩码值为0，添加扰动的区域值为1。

RP\(_{2}\)进一步引入了基于不可印刷性分数（Non-Printability Score，NPS） (Sharif et al., 2016) 的约束条件，用来解决打印机无法打印某些色彩的问题。综合以上技术，RP\(_{2}\)攻击定义如下：

(3.1.54)¶\[\underset{\boldsymbol{\delta}}{\mathop{\mathrm{arg\,min}}} \lambda\left\|M_{{\boldsymbol{x}}} \cdot \boldsymbol{\delta}\right\|_{p}+NPS +\mathbb{E}_{{\boldsymbol{x}}_{i} \sim X^{V}} \mathcal{L}\left(f_{\theta}\left({\boldsymbol{x}}_{i}+T_{i}\left(M_{{\boldsymbol{x}}} \cdot \boldsymbol{\delta}\right)\right), y_{t}\right)\]

其中，\(T_{i}(\cdot)\)是用于将目标变换映射到对抗扰动的对齐函数。在生成完对抗图案后，攻击者可以将生成结果打印出来，并把扰动裁剪出来放到目标物体\(o\)上，如图3.1.6 所示，可以将扰动伪装成常见的海报、涂鸦和黑白格等贴在道路标志牌上。

图3.1.6 RP\(_{2}\)生成的三类物理对抗交通指示牌 (Eykholt et al., 2018)¶

在实景驾驶测试实验中，RP\(_{2}\)在对象受限的海报打印攻击（直接打印整个对象）和贴纸攻击（以贴纸的形式产生扰动，将修改区域限制在一块类似涂鸦或艺术效果的区域中）任务上都取得了不错的攻击成功率，证明生成在不同距离和角度下都能保持对抗性的物理对抗样本是可行的。

对抗补丁（Adversarial Patch，AdvPatch）攻击 (Brown et al., 2017) 是一种基于补丁的物理攻击方法，其对图片的局部区域进行较大幅度的对抗扰动，生成具有强对抗性的补丁。由于扰动幅度很大，对抗补丁可以被打印出来用于在物理场景中攻击深度学习模型，比如使物体检测模型忽略特定的物体并预测错误的类别。

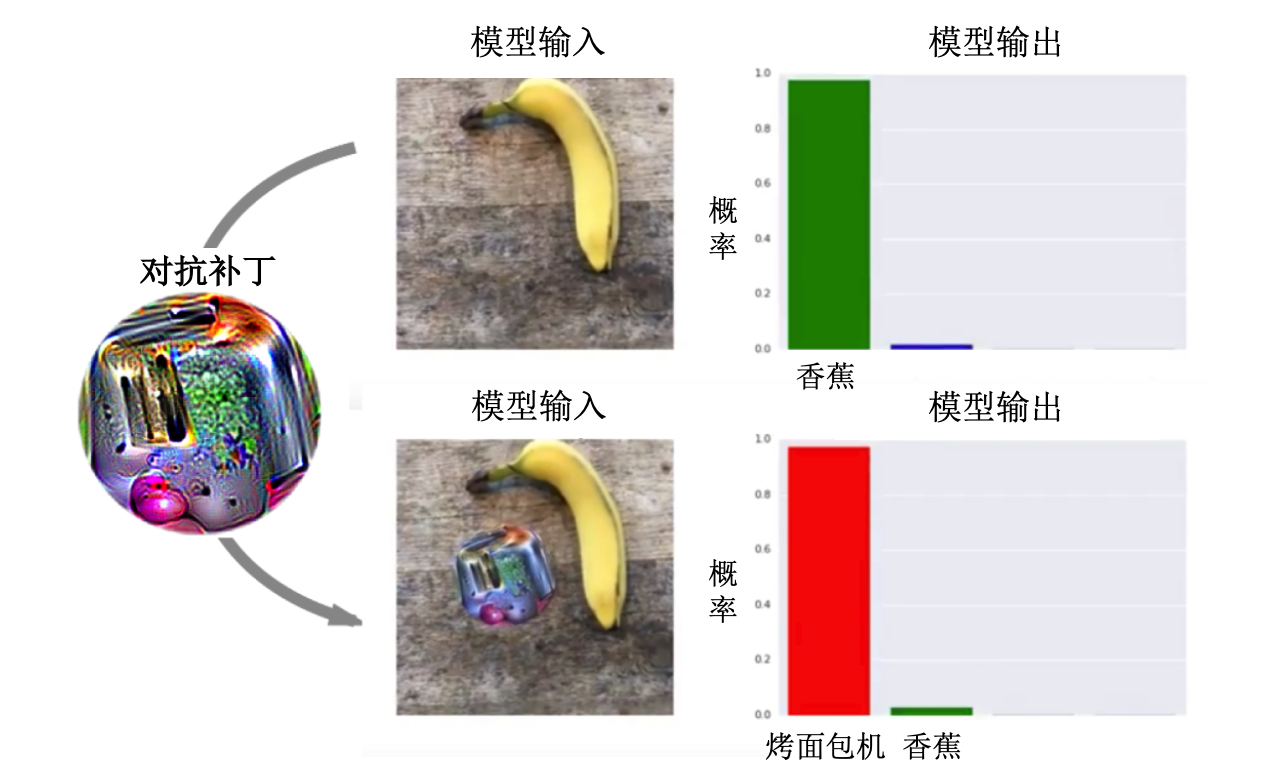
图3.1.7 对抗补丁攻击效果示意图 (Brown et al., 2017)¶

不同于传统梯度优化的算法，AdvPatch用生成的补丁替换图像中的一部分来实现攻击。给定一张图片\({\boldsymbol{x}} \in \mathbb{R}^{w \times h \times c}\)，一个补丁\({\boldsymbol{r}}\)，补丁位置\(l\)和补丁变换\(t\)（如旋转和缩放等），定义打补丁操作\(A({\boldsymbol{r}}, {\boldsymbol{x}}, l, t)\)，先将变换\(t\)应用于补丁\({\boldsymbol{r}}\)，然后将变换后的补丁\({\boldsymbol{r}}\)作用于图片\({\boldsymbol{x}}\)的位置\(l\)上。为了模拟物理环境中的各种条件变化，AdvPatch使用了一种变换期望（Expectation Over Transformation，EOT）算法 (Athalye et al., 2018) 来获得训练后的补丁\(\widehat{{\boldsymbol{r}}}\)。EOT算法通过模拟和求期望来拟合现实世界中的各种变换：

(3.1.55)¶\[\widehat{{\boldsymbol{r}}}=\mathop{\mathrm{arg\,max}}_{{\boldsymbol{r}}} \mathbb{E}_{{\boldsymbol{x}} \sim X, t \sim T, l \sim L}[\log p(\widehat{y} \mid A({\boldsymbol{r}}, {\boldsymbol{x}}, l, t)]\]

其中，\(X\)是图片训练集，\(T\)是补丁变换分布，\(L\)是图像中位置的分布。此外，AdvPatch还添加了一个扰动大小约束\(\left\|{\boldsymbol{r}}-{\boldsymbol{r}}_{\text{orig }}\right\|_{\infty}<\epsilon\)，确保对抗补丁的变化不至于太大。在物理实验中，研究人员将生成的补丁通过标准彩色打印机进行打印，并将它放到不同的场景中进行测试，结果表明这样的补丁能够轻易欺骗分类模型。图3.1.7 展示了对抗补丁进行物理攻击的例子。

对抗风格 对抗补丁的出现大大增加了人工智能模型在真实环境中的安全风险，因为这样的补丁可能以任何形式出现在任何地方。但是AdvPatch攻击生成的补丁风格异常，很容易被察觉。为了提升物理攻击的隐蔽性和自然性，对抗伪装攻击（Adversarial Camouflage, AdvCam） (Duan et al., 2020) 提出将大小不受限的对抗扰动伪装成一种自然的风格，使之看起来是自然的、合理的，从而不容易引起人们注意。图3.1.8 展示了对抗伪装的基本思想，其通过选择现实场景中交通指示牌的不同风格，如褪色、积雪覆盖和生锈等，将对抗性隐藏在不同的风格中，使生成的对抗样本更像自然产生的状态。

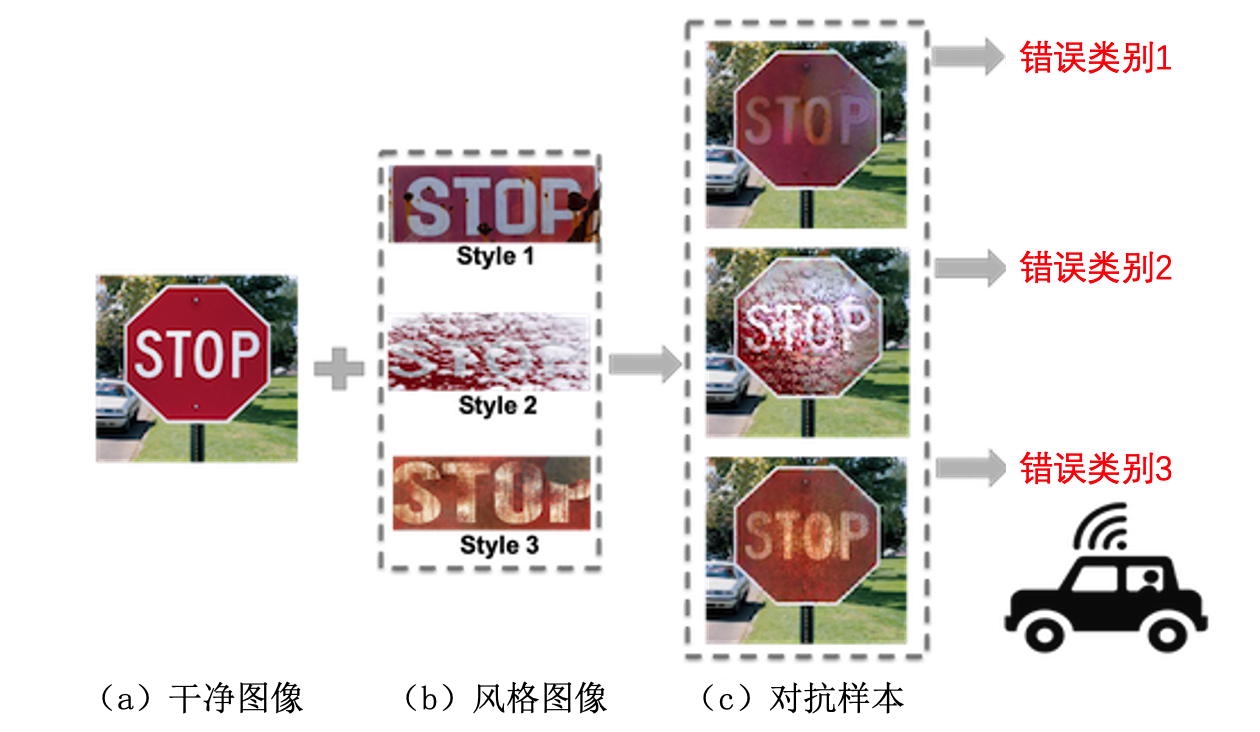
图3.1.8 对抗伪装攻击示意图 (Duan et al., 2020)¶

AdvCam攻击需要同时完成多个任务，使用的损失函数包括：确保对抗性的对抗损失\(\mathcal{L}_{adv}\)、进行风格伪装的风格损失\(\mathcal{L}_s\)、保护原图内容的内容损失\(\mathcal{L}_c\)和平滑对抗扰动的平滑损失\(\mathcal{L}_m\)：

(3.1.56)¶\[\mathcal{L}=\left(\mathcal{L}_{s}+\mathcal{L}_{c}+\mathcal{L}_{m}\right)+\lambda \cdot \mathcal{L}_{adv}\]

其中，对抗样本\({\boldsymbol{x}}'\)和风格参考图片\({\boldsymbol{x}}^s\)之间的风格距离可表示如下：

(3.1.57)¶\[D_{s}=\sum_{l \in {\mathcal{S}}_{l}}{\lVert {\mathcal{G}}\left(\widetilde{f}_{l}\left({\boldsymbol{x}}^{s}\right)\right)-{\mathcal{G}}\left(\widetilde{f}_{l}\left({\boldsymbol{x}}'\right)\right) \rVert}_{2}^{2}\]

其中，\(\widetilde{f}\)表示特征提取器，\({\mathcal{G}}\)是从\(\widetilde{f}\)的风格层（深度神经网络的某些层与风格相关）中提取的风格特征Gram矩阵，并使用掩码矩阵\(M\)来确保只有指定区域（适合进行风格变换的区域）被改变。

上述风格损失\(\mathcal{L}_s\)可以使模型根据参考风格（预先指定的一张风格图片）来生成对抗样本，这有可能会损失原始图像中的部分内容。原始图像的内容可以通过以下损失来保留：

(3.1.58)¶\[\mathcal{L}_{c}=\sum_{l \in {\mathcal{C}}_{l}}{\lVert \widetilde{f}_{l}({\boldsymbol{x}})-\widetilde{f}_{l}({\boldsymbol{x}}') \rVert}_{2}^{2}\]

其中，\({\mathcal{C}}_{l}\)表示用于提取内容特征的神经网络层集合，这保证了对抗样本和原始图像在深层特征空间的相似性。此外，AdvCam攻击还通过减少相邻像素之间的变化来提高对抗图案的平滑度，具体损失公式如下：

(3.1.59)¶\[\mathcal{L}_{m}=\sum(({\boldsymbol{x}}'_{i, j}-{\boldsymbol{x}}_{i+1, j})^{2}+({\boldsymbol{x}}'_{i, j}-{\boldsymbol{x}}^{2}_{i, j+1}))^{\frac{1}{2}}\]

其中，\({\boldsymbol{x}}'_{i, j}\)表示图像\({\boldsymbol{x}}'\)坐标\((i, j)\)处的像素值。最后，对抗损失可以用交叉熵损失来定义：

(3.1.60)¶\[\begin{split}\mathcal{L}_{adv}= \begin{cases}\log p_{y_t}({\boldsymbol{x}}') & \text { 有目标攻击 } \\ -\log p_{y}({\boldsymbol{x}}') & \text { 无目标攻击}\end{cases}\end{split}\]

由于物理环境经常会涉及各种状态波动，如视点偏移、相机噪声和其他变换等，AdvCam同样采用变换集合和EOT算法来模拟物理世界中的多变情况：

(3.1.61)¶\[\min _{{\boldsymbol{x}}'}(\left(\mathcal{L}_{s}+\mathcal{L}_{c}+\mathcal{L}_{m}\right)+\max_{T \in \mathcal{T}} \lambda \cdot \mathcal{L}_{adv}\left({\boldsymbol{x}}_{bg}+T\left({\boldsymbol{x}}'\right)\right)\]

其中，\({\boldsymbol{x}}_{bg}\)表示一张从现实世界中采样的随机背景图片，\(T\)代表一系列随机变换，如旋转、尺寸调整和颜色转换等。实验表明这种结合了风格迁移和对抗攻击的算法可以让对抗样本的隐匿方式更加灵活。

对抗T恤 上述物理攻击都是针对不易形变的刚性物体，如道路标识牌等。在一般情况下这些物体是静止的，贴在其表面的对抗图案不会产生形变，导致这些算法在容易形变的非刚性物体上效果有限。针对此问题，研究人员提出对抗T恤（Adversarial T-shirts，AdvTShirt）攻击 (Xu et al., 2020) ，使得对抗样本在T恤这类会随人类姿态和动作的变化而发生形变的非刚性物体上也能发挥作用。当攻击者穿上印有对抗图案的T恤后能躲过物体检测模型，使其无法检测到攻击者的存在。图3.1.9 展示了该算法生成的对抗T恤在数字和物理世界中攻击物体识别模型YOLOv2时的有效性。

为了适应物理环境变化，AdvTShirt攻击进一步将期望转换算法（即EOT）推广到对抗性T恤的设计。如前文所述，该方法将可能发生在现实世界中的多种变化，如缩放、旋转、模糊、光线、噪声等，通过模拟和求期望来拟合现实，且在刚性物体上有不错的效果。但该方法无法模拟T恤在人体运动时产生的褶皱形变，而这种形变会使对抗样本失去作用。于是，AdvTShirt攻击设计了一种基于薄板样条插值（Thin Plate Spline，TPS）的变换算法来模拟由人体姿态变化引起的T恤变形，TPS算法已被广泛用于图像对齐和形状匹配中的非刚性变换模型。

图3.1.9 数字和物理对抗T恤成功躲避物体检测模型 (Xu et al., 2020)¶

图3.1.10 展示了该算法的总体流程。具体地，以视频中的两帧为例，有一个锚点图像\({\boldsymbol{x}}_0\)和一个目标图像\({\boldsymbol{x}}_i\)，对于\({\boldsymbol{x}}_0\)中给定的人物边界框\(M_{p, 0} \in\{0,1\}^{d}\)和T恤边界框\(M_{c, 0} \in\{0,1\}^{d}\)，使用从\({\boldsymbol{x}}_0\)到\({\boldsymbol{x}}_i\)的透视变换来获得图像\({\boldsymbol{x}}_i\)中的人物边界框\(M_{p, i}\)和T恤边界框\(M_{c, i}\)。于是，尚未考虑物理变换的关于\({\boldsymbol{x}}_i\)的扰动图像\({\boldsymbol{x}}'_{i}\)可表示为：

(3.1.62)¶\[{\boldsymbol{x}}'_{i}=\underbrace{\left(\mathbf{1}-M_{p, i}\right) \circ {\boldsymbol{x}}_{i}}_{\text{A}}+\underbrace{M_{p, i} \circ {\boldsymbol{x}}_{i}}_{\text{B}}-\underbrace{M_{c, i} \circ {\boldsymbol{x}}_{i}}_{\text{C}}+\underbrace{M_{c, i} \circ \boldsymbol{\delta}}_{\text{D}}\]

其中，A项表示人物边框外的背景区域，B项是人物边界区域，C项表示删除T恤边界框内的像素值，D项是新引入的加性扰动。该公式可简化为对抗样本的常规表示：\(\left(1-M_{c, i}\right) \circ {\boldsymbol{x}}_{i}+M_{c, i} \circ \boldsymbol{\delta}\)。

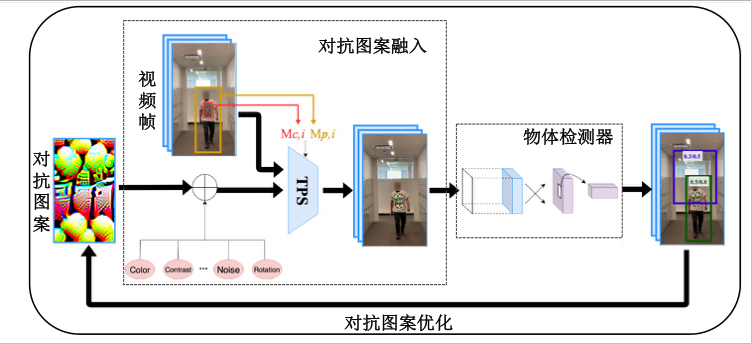
../_images/6.10_adv_tshirt_framework.png

图3.1.10 对抗T恤生成流程图 (Xu et al., 2020)¶

接下来，AdvTShirt考虑三种类型的物理转换：（1）对扰动 \(\boldsymbol{\delta}\)进行TPS转换\(t_{TPS} \in {\mathcal{T}}_{TPS}\)，以此来模拟布料变形的影响；（2）物理颜色转换\(t_{color}\)，这种转换可将数字颜色转换为在物理世界中可被打印出来的颜色；（3) 应用于人物边框内区域的常规物理变换\(t \in {\mathcal{T}}\)。这里\({\mathcal{T}}_{TPS}\)表示非刚性变换集合，\(t_{color}\)由一个可将数字空间色谱映射到对应的印刷品的回归模型给出，\({\mathcal{T}}\) 表示常用的物理变换集合，包括缩放、平移、旋转、亮度、模糊和对比度等。综合考虑以上不同物理转换后的算法公式为：

(3.1.63)¶\[{\boldsymbol{x}}'_{i}=t_{env}\left(\text{A}+t\left(\text{B}-\text{C}+t_{color}\left(M_{c, i} \circ t_{TPS}(\boldsymbol{\delta}+\mu {\boldsymbol{v}})\right)\right)\right)\]

其中，\(t \in {\mathcal{T}}\),\(t_{TPS} \in {\mathcal{T}}_{TPS}\)，\({\boldsymbol{v}} \sim {\mathcal{N}}(0,1)\)，\(t_{env}\)表示环境亮度变换，\(\mu {\boldsymbol{v}}\)是允许像素值变化的加性高斯噪声，它可使最终的目标函数更平滑，更有利于优化过程中的梯度计算，\(\mu\)是给定的平滑参数。

最终，用于欺骗单个检测器的期望转换公式为：

(3.1.64)¶\[\underset{\boldsymbol{\delta}}{\min} \;\; \frac{1}{M} \sum_{i=1}^{M} \mathbb{E}_{t, t_{TPS}, {\boldsymbol{v}}}\left[\mathcal{L}_{adv}\left({\boldsymbol{x}}'_{i}\right)\right]+\lambda g(\boldsymbol{\delta})\]

其中，\(\mathcal{L}_{adv}\)是提升错误检测的对抗损失，\(g\)是增强扰动平滑度的变分范数（Total Variation norm，TV-norm），\(\lambda>0\) 是正则化参数。实验表明，通过上述算法生成的对抗T恤在数字和物理世界中对物体检测模型YOLOv2的攻击成功率可分别达到74%和 57%，相比之前方法有巨大提升。

3D对抗物体 对抗T恤探索了如何将对抗图案放在衣服上的问题，这里MSF-ADV攻击（Multi-sensor Fusion Adversarial attack） (Cao et al., 2021) 则探索了如何设计3D对抗物体来攻击真实场景下的自动驾驶系统。雷达和摄像头是自动驾驶常用的两种传感器，其捕获的路面信息和路况信息在分别处理后会通过两个不同的网络进行一定的融合和对齐，融合得到的信息用来支撑自动驾驶的决策。图3.1.11 展示了MSF-ADV攻击流程，其主要思想是充分利用两类传感器的特点生成具有对抗性的三维物体，通过优化物体的3D角度、位置、表面平滑度等性质，使其更容易在物理世界实现（比如3D打印）并保持对抗性。其中，主要的难点包括对雷达模块信息处理（即3D点云处理）的可微近似、点云信息与图像信息的匹配以及对抗形状的优化等。此研究工作第一次完整的攻破了自动驾驶的雷达和摄像头两个感知系统，在模拟自动驾驶场景中可以误导企业级的自动驾驶汽车撞上3D对抗物体。

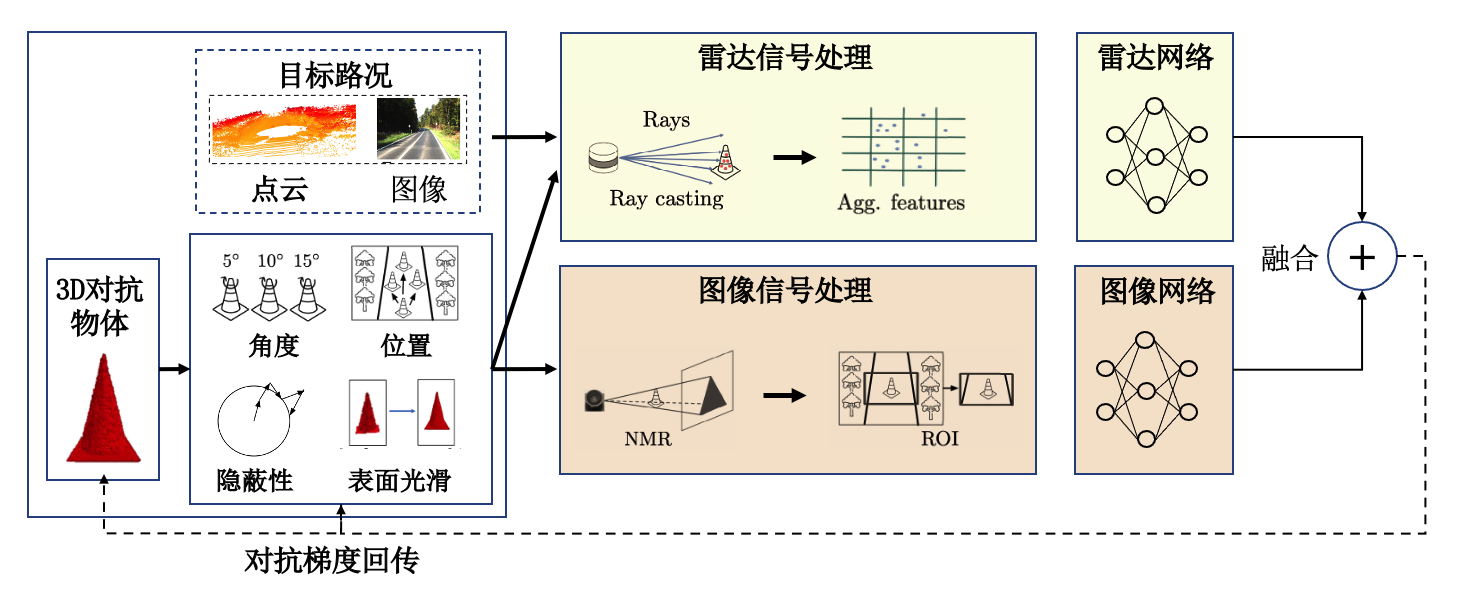
图3.1.11 多传感器融合攻击流程图 (Cao et al., 2021)¶

3.2. 数据投毒¶

数据投毒（也称投毒攻击）是一种训练阶段的攻击，其通过污染训练数据来破坏模型的训练，从而达到降低模型性能的目的。投毒攻击的一般流程如图3.2.1 所示。在实际场景中，投毒者可以通过两种方式实施投毒攻击，即被动攻击和主动攻击。被动攻击是指攻击者可通过在线社交媒体上传有毒数据，等待受害者利用网络爬虫下载使用；主动攻击则可以直接将有毒数据发送到数据集收集器中（如聊天机器人、垃圾邮件过滤器或用户信息数据库）。研究机构对28家公司的调查问卷显示数据投毒是工业界最担心的人工智能安全问题 (Kumar et al., 2020) 。

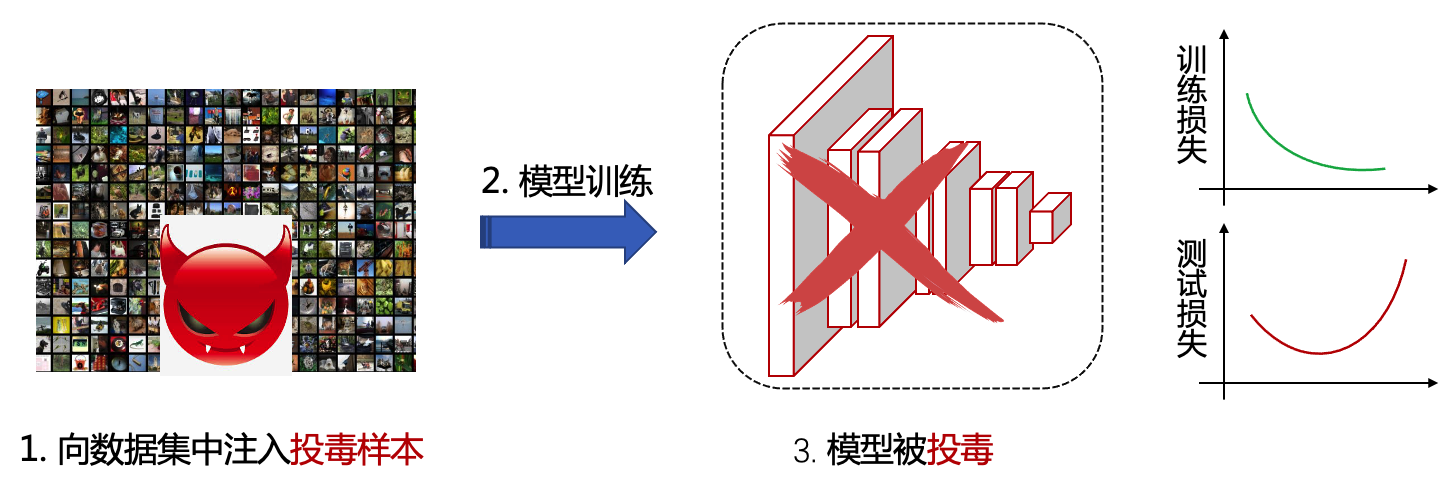
图3.2.1 投毒攻击示意图¶

数据投毒研究最早可以追溯到1993年Kearns和Li的工作 (Kearns and Li, 1993) ，他们在PAC（Probably Approximately Correct）学习设置下研究了如何在有恶意误差数据存在的情况下进行模型训练。 2006 年，Barreno等人 (Barreno et al., 2006) 揭示了通过恶意训练人工智能系统可以混淆网络入侵检测系统，使其在推理阶段对特定攻击不作拦截。2008年，Nelson等人 (Nelson et al., 2008) 提出了针对垃圾邮件过滤器的投毒攻击，通过错误标记1%的训练数据成功破坏了朴素贝叶斯（Naive Bayes）分类器的垃圾邮件过滤功能。2012年，Biggio等人 (Biggio et al., 2012) 正式提出了投毒攻击的概念，特指一类将小部分毒化数据注入到训练数据集或直接投毒模型参数进而损害目标系统功能的攻击。

根据已有工作，数据投毒攻击算法可大致分为六类：标签投毒攻击、在线投毒攻击、特征空间攻击、双层优化攻击、生成式攻击和差别化攻击。

3.2.1. 标签投毒攻击¶

模型训练是一个在训练样本上进行迭代，使模型预测能够一步步靠近真实标签的过程。所以正确的标签对模型训练至关重要，而这正是投毒攻击者重点攻击的点。毋庸置疑，模型训练所使用的标签信息是最直接的一种投毒方式，而这种攻击也被称为标签投毒攻击（Label Poisoning Attack，LPA）。LPA通过混淆样本与标签之间的对应关系来破坏模型的训练。例如，标签翻转攻击（Label Flipping，LF）将部分二分类数据的\(0\)/\(1\)标签进行随机翻转，使\(0\)标签对应数据在训练中靠近假标签\(1\)，而\(1\)标签对应数据靠近假标签\(0\)。可以看出，此类投毒攻击需要很强的假设，要求投毒者可以操纵训练数据的标注或使用。在二分类问题下，随机标签翻转攻击可形式化表示为：

(3.2.1)¶\[\begin{split}LF(y) =\begin{cases}& 1-y, \;\; y\in Y =\{0,1\} \\& \text{random}( Y/\{y\}), \; \text{ otherwise}\end{cases}\end{split}\]

其中，\(y\)是原始标签，\(1-y\)可以在0-1分类问题下进行类别的翻转，\(\text{random}(\cdot)\)表示随机选择函数，适用于多分类问题。

除了随机选择样本翻转，攻击者还可以有选择性地对一部分关键数据进行标签翻转以最大化攻击效果。例如，可以通过特定优化方法寻找部分易感染样本进行标签翻转 (Biggio et al., 2012) 。标签投毒类攻击可以被理解为是一种“指鹿为马”攻击，明明是物体A却说成是物体B，从而达到混淆视听的目的。

3.2.2. 在线投毒攻击¶

p-篡改攻击（\(p\)-tampering attack）是一个经典的在线投毒攻击方法，其在在线学习过程中对训练样本以一定概率\(p\)进行投毒，并以此削弱模型推理能力的攻击。p-篡改攻击假设攻击者可以对训练样本进行在线的修改、注入等，但对标签不作改动。最早将\(p\)篡改攻击用于数据投毒的是Mahloujifar和Mahmoody (Mahloujifar and Mahmoody, 2017) ，他们以在线训练中的一段训练数据为原子，对其中比例为\(p\)的数据施加噪声来进行偏置，进而对模型在推理阶段的功能进行干扰。\(p\)篡改攻击可以被理解为是一种“暗度陈仓”攻击，在不改变类别标签（故隐蔽性高）的情况下，以一定概率偷偷修改样本，使数据分布产生偏移。

Mahloujifar等人 (Mahloujifar et al., 2019) 后续将单方\(p\)-篡改攻击扩展到了多方学习，并以联邦学习为例进行了研究。不同于单方学习，多方学习中参与方之间会相互影响，给数据投毒留下了很多空间（可相互传染）也带来一些挑战（避免相互干扰）。在多方学习场景下，\(p\)-篡改攻击可以扩展到\((k,p)\)-篡改攻击，其中\(k\in\{1,2,\cdots,m\}\)表示\(m\)个参与方中被攻击者控制的个数。\((k,p)\)-篡改可以高效地完成攻击，且不需要修改标签，是一种只依赖当前时刻样本的高效在线投毒攻击。

3.2.3. 特征空间攻击¶

特征空间投毒（Feature Space Poisoning，FSP）攻击通过修改毒化样本的深度特征来完成攻击。通过基于替代模型的深度特征修改，特征空间攻击几乎可以随意修改样本与类别之间的对应关系，即能让一个类别为A的样本跟任意非A类别的深度特征匹配。特征空间攻击有三个隐蔽性优势。首先，在特征空间进行对应关系的修改并不需要修改标签，具有很高的隐蔽性。其次，特征投毒可以基于优化方法通过对输入样本的微小扰动完成，并不需要明显的投毒图案，因此可轻易躲过人工审查。第三，特征空间攻击通常只影响模型对特定目标样本的分类，而不影响非特定目标样本，故而很难被检测出来。毒化数据的影响通常在模型部署后才会显现出来。

特征碰撞攻击（Feature Collision Attack，FCA） (Shafahi et al., 2018) 是一个经典的特征空间投毒方法。特征碰撞攻击是一种白盒数据毒化方法，其通过扰动部分基类（base class）训练数据，使其在特征空间下趋于目标类（target class），从而诱导模型在训练过程中产生误解。特征碰撞攻击最初是为攻击单个目标样本而设计的，攻击多个样本则需要多次执行同样的攻击过程。

具体而言，特征碰撞攻击巧妙地使有毒基类数据点在特征空间中靠近目标类样本，从而诱使目标模型在推理阶段将目标类测试样本误分为基类类别。特征碰撞攻击的优化目标定义如下：

(3.2.2)¶\[\underset{{\boldsymbol{x}}_p}{\min}\Big[{\lVert f({\boldsymbol{x}}_p)-f({\boldsymbol{x}}_t) \rVert}^2_2+\beta {\lVert {\boldsymbol{x}}_p-{\boldsymbol{x}}_b \rVert}^2_2\Big]\]

其中，\({\boldsymbol{x}}_p\)为毒化样本，\({\boldsymbol{x}}_t\)为目标测试样本，\({\boldsymbol{x}}_b\)为训练数据中一个基类样本，\(f\)表示目标模型，\(f(\cdot)\)为模型的输出，\(\beta\)为超参数。上式中，第一项使毒化样本接近攻击目标类别\(t\)，达成攻击目的；第二项\({\lVert {\boldsymbol{x}}_p-{\boldsymbol{x}}_b \rVert}^2_2\)控制毒化数据与基类数据相似，使二者在视觉上无明显差异，提升隐蔽性。通俗的理解就是，让\({\boldsymbol{x}}_p\)看上去像\({\boldsymbol{x}}_b\)而特征和预测类别像\({\boldsymbol{x}}_t\)，起到“声东击西”的目的。后续很多隐蔽性数据投毒算法都是基于此思想，只是在优化方法上有所不同。

在特征碰撞攻击中，目标模型通常是在干净数据上预训练的模型，而投毒攻击发生在后续的模型微调过程中，主要用于攻击基于公开预训练模型的迁移学习。由于迁移学习冻结特征提取器而只微调最后一层的线性分类器，所以特征碰撞攻击对迁移学习很有效，有时毒化单张图像就可以成功攻击。然而，特征碰撞攻击也存在一定的局限性。首先，特征碰撞攻击需要攻击者掌握目标模型，这是一个并不太现实的假设。其次，一旦目标模型又通过其他干净数据再次微调，那么特征攻击效果会大大降低。因此，端到端训练或逐层微调对特征碰撞攻击具有显著的鲁棒性。

凸多面体攻击（Convex Polytope Attack，CPA） (Zhu et al., 2019) 是一种不修改标签的特征空间攻击。与特征碰撞攻击的单样本混淆策略不同，凸多面体攻击尝试寻找一组毒化样本将目标样本包围在一个凸包内。凸多面体攻击的优化目标如下：

(3.2.3)¶\[\begin{split}\begin{split}\min\limits_{\{c^{(i)}\},\{{\boldsymbol{x}}^{(j)}_p\}} & \frac{1}{2m}\sum^m_{i=1}\frac{\left\|f^{(i)}({\boldsymbol{x}}_t)-\sum^k_{j=1}c^{(i)}_j f^{(i)}({\boldsymbol{x}}^{(j)}_p)\right\|^2}{\left\|f^{(i)}({\boldsymbol{x}}_t)\right\|^2} \\s.t. \; & \sum^k_{j=1}c^{(i)}_j=1, c^{(i)}_j\geq0, \forall i,j; \; \left\|{\boldsymbol{x}}^{(j)}_p-{\boldsymbol{x}}^{(j)}_b\right\|_\infty\leq\epsilon, \forall j\end{split}\end{split}\]

其中，\({\boldsymbol{x}}_p\)为毒化样本，\({\boldsymbol{x}}_t\)为目标测试样本，\({\boldsymbol{x}}_b\)为训练数据中一个基类样本；一组预训练模型的集合被定义为\(\{f^{(i)}\}^m_{i=1}\)，\(m\)是集合中模型的数量；\(\{{\boldsymbol{x}}^{(j)}_p\}^k_{j=1}\)是针对\({\boldsymbol{x}}_t\)设计的\(k\)个“包围”样本，约束\(\sum^k_{j=1}c^{(i)}_j=1, c^{(i)}_j\geq0\)指\(k\)包围样本的权重都大于0且加和为1；添加扰动的上界被定义为\(\epsilon\)。凸多面体攻击在特征空间中构建了更大的“攻击区域”，从而增加了迁移攻击成功的可能性。当在多个中间层中实施凸多面体攻击时，迁移性会更大。凸多面体攻击可以被理解为是一种“四面楚歌”的攻击方式，从不同角度对特征子空间进行围攻，从而使投毒数据在从头训练时也能起作用。

3.2.4. 双层优化攻击¶

近期的研究往往通过双层优化的方式去实现数据投毒，这种策略可以与其他攻击方式结合产生更大效益。实际上，优化的思想在数据投毒中早已存在，比如通过优化方法找出最适合标签投毒的数据集或者找到最有效的数据投毒方案。早在2008年，Nelson等人 (Nelson et al., 2008) 便在其工作中通过优化产生能最大化合法邮件有害得分的电子邮件，并用来毒化训练数据。2012年，Biggio等人 (Biggio et al., 2012) 同样也使用了优化方法来找到可以最大化分类误差的样本。上述两种方法都是利用基于梯度上升的迭代算法来一步步计算出最优解决方案，并更新迭代出最终目标模型。为了统一概括数据投毒的优化问题，Mei和Zhu (Mei and Zhu, 2015) 在2015年正式提出了“有毒数据构建+目标模型更新”的双层优化（bi-level optimization）问题，并证明利用梯度可以有效地解决此问题。此后，数据投毒攻击便进入了双层优化时代，研究者陆续提出更有效、更快速、抑或更便捷的数据投毒攻击方法。

双层优化攻击所对应的问题一般是一个最大最小化问题（max-min），一般通过下面两步来解决：（1）攻击者首先将投毒攻击问题转化为一个优化问题；（2）攻击者使用常见优化算法（如随机梯度下降）在相应的约束下解决优化问题。数据投毒对应的双层优化问题可形式化为：

(3.2.4)¶\[\begin{split}\begin{aligned}& {D_p}' = \underset{D_p}{\mathop{\mathrm{arg\,max}}} \, {\mathcal{F}}(D_p, { \theta}' ) = \mathcal{L}_{out}( D_{val},\theta' ) \\& s.t. \;\; \theta' = \underset{\theta}{\mathop{\mathrm{arg\,min}}} \, \mathcal{L}_{in}(D\cup D_{p}, \theta)\end{aligned}\end{split}\]

其中，\(D\)、\(D_{val}\)及\(D_{p}\)分别表示原始训练数据、验证数据以及有毒数据，\(\mathcal{L}_{in}\)和\(\mathcal{L}_{out}\)分别代表内层和外层的损失函数。外层优化的目的是生成有毒数据，使其可以最大化验证数据集\(D_{val}\)（此数据集是干净的）在目标模型\(\theta'\)上的分类错误。内层优化的目的是训练目标模型，即目标模型会在有毒数据集\(D\cup D_p\)上迭代更新。由于目标模型参数\(\theta'\)是由有毒数据集\(D_{p}\)来隐式决定的，所以在外层优化中，我们用函数\({\mathcal{F}}\)来表述\(\theta'\)和\(D_{p}\)之间的联系。整个双层优化的过程可以描述为，每当内层优化达到局部最小值，外层优化会用更新后的目标模型\(\theta'\)来更新有毒数据集\(D_{p}\)，直到外层优化的损失函数\(\mathcal{L}_{out}( D_{val},\theta' )\)收敛。

双层优化攻击是一种无目标投毒攻击，因为其攻击目标是让目标模型发生任意分类错误。当然，双层优化攻击也可以是有目标的，即让目标模型将目标数据误分类为特定类别。在这种情况下，双层优化就变成了一个最小最小化问题（min-min），定义如下：

(3.2.5)¶\[\begin{split}\begin{aligned}& {D_p}' = \underset{D_p}{\mathop{\mathrm{arg\,min}}} \, {\mathcal{F}}( D_p, { \theta}' ) = \mathcal{L}_{out}( \left\{{\boldsymbol{x}}_t, y_{adv}\right\} , \theta' ) \\& s.t. \;\; \theta' = \underset{\theta}{\mathop{\mathrm{arg\,min}}} \, \mathcal{L}_{in}(D\cup D_{p}, \theta )\end{aligned}\end{split}\]

其中，\(y_{adv}\)是攻击者预设的错误类别。而此时外层优化的目的是生成可以最小化目标模型\(\theta'\)在目标数据上的分类错误的有毒数据。上面的双层优化框架很好地概括了数据投毒与目标模型更新之间的关系，通过代入不同的目标函数、攻击目标及训练数据集，几乎所有数据投毒攻击场景都可以用这个框架实现。

解决双层优化问题的一种思路是通过迭代算法来步步逼近全局最优解。而基于梯度的攻击又可以将训练数据往目标梯度方向扰动进行数据毒化，直至毒化数据达到最优效果。在\(\mathcal{L}_{out}\)可微的情况下，梯度可以通过链式法则（chain rule）计算如下：

(3.2.6)¶\[\begin{split}\begin{aligned}& \nabla_{D_p} {\mathcal{F}} = \nabla_{D_p} \mathcal{L}_{out} + \frac{\partial \theta}{\partial D_p}^{\top}\nabla_{\theta}\mathcal{L}_{out} \\& s.t. \;\; \frac{\partial \theta}{\partial D_p}^{\top} = ( \nabla_{D_p} \nabla_{\theta} \mathcal{L}_{in} ) ( \nabla_{\theta}^2 \mathcal{L}_2 )^{-1}\end{aligned}\end{split}\]

其中，\(\nabla_{D_p}{\mathcal{F}}\)表示\({\mathcal{F}}\)关于\(D_p\)的偏导数。第\(i\)次迭代的毒化数据\(D_p^{(i)}\)可以通过梯度上升更新至\(D_p^{(i+1)}\)，形式化定义如下：

(3.2.7)¶\[D_p^{(i+1)} = D_p^{(i)} + \alpha\nabla_{D_p^{(i+1)}}{\mathcal{F}}( D_p^{(i)} )\]

其中，\(\alpha\)是由攻击者控制的学习率。

MetaPoison攻击 (Huang et al., 2020) 采用集成的方式，利用\(m\)个模型和\(K\)-step内部最小化来求解式 (3.2.5) 。具体来说，对每个模型在毒化数据上进行\(K\)步基于SGD的梯度下降，然后计算并存储外部最小化对应的梯度（称为对抗梯度），在\(m\)个模型上计算完毕后累积得到平均对抗梯度，之后使用平均对抗梯度更新毒化样本。当达到一定的训练周期后，需要重新初始化\(m\)个模型的参数，以增加探索（防止因模型收敛过快而导致毒化样本探索不够）。

MetaPoison是干净标签数据投毒（clean-label data poisoning）领域的一个重要改进。其数据毒化过程更加通用，无论是无目标还是有目标攻击都可达成，生成的毒化数据可以在整个训练过程中都对目标模型有影响，而且不会对某个代理模型过拟合。此外，MetaPoison还做到了毒化数据的跨模型和训练设置迁移，即MetaPoison生成的毒化数据可投毒其他训练设置和架构的模型。MetaPoison甚至成功毒化了工业级服务（Google Cloud AutoML API）。而MetaPoison也是第一个在人眼不可察觉的前提下，可同时攻击微调模型及端到端模型的数据投毒方法。

女巫酿造攻击（Witches\('\) Brew） (Geiping et al., 2021) 对MetaPoison攻击作了进一步改进，使得此类投毒攻击达到工业规模。女巫酿造攻击引入梯度对齐的概念，使毒化目标函数与对抗目标函数具有一致的梯度，也就是说，使模型在毒化样本和其目标样本上的梯度一致。当这个目标达成时，毒化样本和目标样将对模型产生同样的梯度激活，也就是在训练过程中对模型参数更新起到一模一样的作用，因此训练毒化数据过程中进行的标准梯度下降也会强制使对应目标图像上的对抗性损失降低，进而完成攻击目标（让模型将毒化样本完全当作目标样本来学习）。

3.2.5. 生成式攻击¶

上述数据投毒攻击都在毒化数据生成和使用效率上有所受限，而基于生成模型的生成式攻击则可避免基于优化攻击的高昂计算代价，大大提高毒化数据的生成和使用效率。生成式攻击的核心是生成模型的训练。生成模型可以通过学习毒化噪声分布进而大规模生成毒化数据。生成式攻击一般需要攻击者知晓目标模型的相关知识，对应灰盒或白盒威胁模型。

基于自动编解码器的投毒 该攻击 (Yang et al., 2017) 通过训练自动编解码器来生成投毒样本，一般通过两个模型交替优化来完成：生成模型\(G\)以及目标模型\(f\)。毒化数据生成过程可以描述为：在第\(i\)次迭代中，生成模型产生毒化数据\({\boldsymbol{x}}_p^i\)；攻击者将此时的毒化数据注入到训练数据中，令目标模型的参数从\(\theta^{( i-1 )}\)更新为\(\theta^{( i )}\)；攻击者进一步评估目标模型在验证集\(D_{val}\)上的表现，并以此为依据引导生成模型的进一步优化；攻击者更新生成模型并进入下一轮迭代。此迭代过程可形式化表示为：

(3.2.8)¶\[\begin{split}\begin{aligned}& G' = \underset{G}{\mathop{\mathrm{arg\,max}}} \sum_{({\boldsymbol{x}},y)\sim D_{val}} \mathcal{L}( f_{\theta'}( G({\boldsymbol{x}} )), y) \\& s.t. \; \theta' = \underset{\theta}{\mathop{\mathrm{arg\,min}}} \sum_{({\boldsymbol{x}},y)\sim D_{p}} \mathcal{L}( f_{\theta}( G'( {\boldsymbol{x}} ) ), y )\end{aligned}\end{split}\]

其中，\(\theta\)表示目标模型\(f\)的原始参数，\(\theta'\)表示目标模型被数据投毒攻击后的参数。生成式攻击的最终目标是使生成模型\(G\)能够无限生成能降低目标模型\(f\)性能的毒化数据。在两个模型交替更新的过程中会出现节奏不一致问题，即一个更新的快一个更新的慢，导致的生成模型训练不稳定。这种问题可以通过在更新生成模型\(G\)时引入伪更新（pseudo-update） (Feng et al., 2019) 步骤来解决。

基于生成对抗网络的投毒 当然除了自动编码器，生成对抗网络（GAN）也可以用来生成毒化数据。pGAN攻击 (Muñoz-González et al., 2019) 就是一个基于生成对抗网络的数据投毒方法，其由生成器\(G\)，鉴别器\(D\)及分类器（即目标模型\(f\)）三个子模型组成。鉴别器\(D\)用于区分毒化样本与干净样本，而生成器\(G\)旨在生成高效的毒化样本以最大化目标模型\(f\)的分类误差，同时让鉴别器\(D\)无法区别毒化样本与干净样本。这种对抗博弈使得生成式攻击可以在攻击强度和隐蔽性之间作出权衡，更灵活地应对不同风险级别的人工智能模型。

3.2.6. 差别化攻击¶

上述几类攻击方法在投毒的过程中随机选取少量训练样本进行毒化，可以被认为是一种无差别化攻击。然而，研究发现毒化样本的选择会大大影响攻击效果。由此引出了基于样本影响力的差别化攻击。基于样本影响函数（influence function）的投毒攻击通过选择影响力大的样本来投毒，以此来提高攻击的强度。单个样本对模型性能的影响可以定义为：

(3.2.9)¶\[\begin{split}\begin{aligned}& {\mathcal{I}}( {\boldsymbol{z}} ) = -{\boldsymbol{H}}_{\hat{\theta}}^{-1}\nabla_{\theta}\mathcal{L}( f_{\hat{\theta}} ( {\boldsymbol{x}} ), y) \\& s.t. \;\; \hat{\theta} = \underset{\theta}{\mathop{\mathrm{arg\,min}}} \sum_{({\boldsymbol{x}},y) \sim D_{val}}\mathcal{L}( f_{\theta}( {\boldsymbol{x}} ),y )\end{aligned}\end{split}\]

其中，\({\boldsymbol{x}}\)表示目标样本，\(y\)表示样本标签，\(\hat{\theta}\)表示移除样本\({\boldsymbol{x}}\)后所得到的目标模型的参数，\(D_{val}\)表示验证数据集，\({\boldsymbol{H}}\)为经验风险的海森矩阵（Hessian matrix），即\({\mathcal{H}}_{\hat{\theta}}= \frac{1}{n}\sum_{i=1}^{n}\nabla^2_{\hat{\theta}}L( f_{\hat{\theta}}( {\boldsymbol{x}}_i ),y_i )\)。

基于影响函数，可以通过下面几步完成差别化投毒攻击 (Koh et al., 2022) 。首先，通过式 (3.2.9) 来计算删除特定样本对测试损失的影响，进而确定对模型训练影响最大的样本。接下来，以较大影响样本作为毒化目标，继续利用影响函数来产生毒化数据。最后，将毒化数据注入到原始训练数据集中。最终，该方法成功使目标模型将一个特定测试图片错误分类。

3.3. 后门攻击¶

正所谓“病从口入”，数据投毒是最经典的一种后门攻击方式，其通过投毒少部分训练数据，使后门触发器与某个攻击者指定的后门类别建立关联，从而将后门安插到目标模型中去。后门攻击除了可以以数据投毒的方式进行攻击以外，还可以通过操纵训练算法、使用特定的数据增强组合或者干脆直接修改训练后的模型参数来完成。

后门攻击可能会出现在数据收集、模型训练、大规模预训练、下游微调等阶段。考虑到深度神经网络的训练往往需要大量的训练数据，且对计算资源具有较高的需求，普通用户通常难以同时满足上述要求。因此，部分模型开发人员可能选择将训练任务外包给第三方平台，或者直接在公开预训练模型上进行下游任务微调。在此情况下，攻击者可能在第三方平台训练过程中将后门植入到目标模型中。此外，恶意攻击者也可能将包含后门的模型上传至公开平台，如GitHub、HuggingFace等，诱导用户（受害者）下载使用。上述两种场景均为后门攻击的成功实施提供了条件。

3.3.1. 输入空间攻击¶

BadNets攻击 (Gu et al., 2017) 是一种经典的脏标签攻击（即在修改样本的同时需要修改其标签）方法。值得一提的是，基于数据投毒的后门攻击一般假设攻击者只能向训练数据中注入少部分后门样本，但是不能控制模型的训练过程，这里BadNets的威胁模型相对宽松一些，攻击者既可以接触到训练数据又可以控制模型训练。

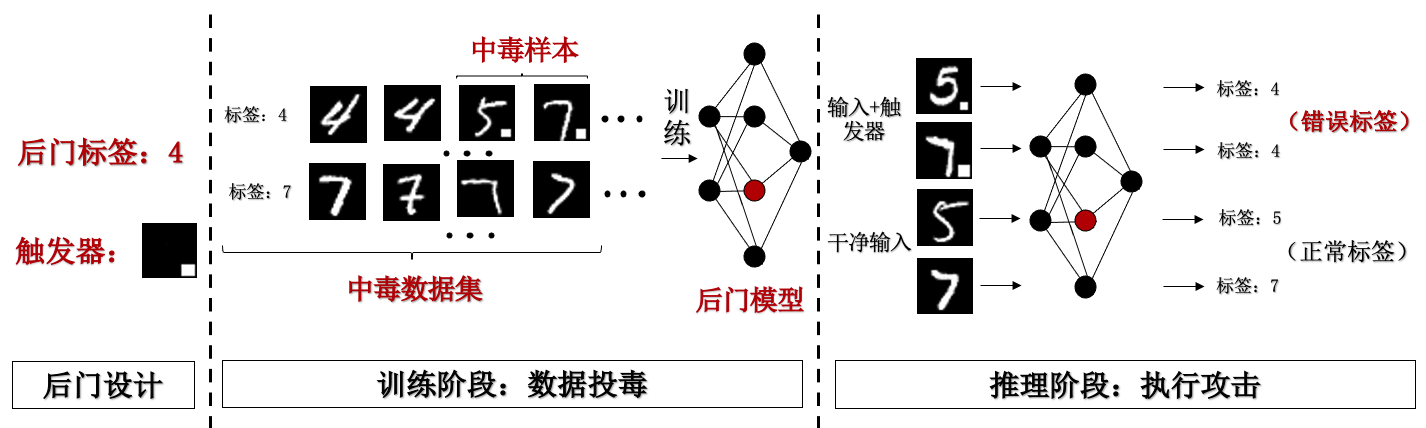
图3.3.1 BadNets攻击流程 (Gu et al., 2017)¶

图3.3.1 展示了BadNets的攻击流程。具体实施策略如下：给定训练集\(D_{train}\)，从\(D_{train}\)中按一定比例\(p\)随机抽取样本，插入后门触发器并修改其原始标签为攻击目标标签\(y_{t}\)，得到后门数据集\(D_{p}\)。被毒化的训练数据集可表示为\(\hat{D}_{train}=D_{c} \cup D_{p}\)，其中\(D_{c}\)表示干净部分数据，\(D_{p}\)表示毒化部分数据。在\(\hat{D}_{train}\)上训练得到的模型即为后门模型。图3.3.1 展示了简单的后门触发器图案：单像素点和白方块。为了满足隐蔽性，这些触发器往往被添加在输入图像的特定区域（如图像右下角）。对图像分类任务来说，在毒化数据集上训练后门模型的过程可定义如下：

(3.3.1)¶\[\min_{\theta} \mathbb{E}_{({\boldsymbol{x}}, y) \sim \hat{D}_{train}}\left[\mathcal{L}_{CE}\left(f_{\theta}({\boldsymbol{x}}), y\right)\right]\]

上述公式给出了后门攻击的一般性优化目标。后续的相关工作大都遵循这一原则，只是在触发器的设计上作不同的改进和提升。另一方面，BadNets攻击主要围绕模型外包和预训练模型场景，这使得此类后门攻击可以影响不同的数据集和模型结构，且不需要很高的投毒率。举例来说，BadNets后门攻击在CIFAR-10数据集上能够以10%以下的投毒率达到99%以上的攻击成功率（当然就现在的研究来说，10%的投毒率已经是很高了）。

Blend攻击 (Chen et al., 2017) 在BadNets攻击的基础上设计了新颖的触发器：全局随机噪声和图像混合策略。Blend攻击的提出，使得后门触发器不再只局限于图像的特定区域（在BadNets攻击中触发器固定在图像的右下角）。基于全局随机噪声的攻击将随机噪声作为后门触发器与干净样本进行叠加；基于图像混合的攻击将指定图像作为后门触发器与干净样本进行叠加。作为一种脏标签攻击，Blend在添加完后门触发器后也需要将图像的标签修改为后门标签。

图3.3.2 随机噪声后门攻击 (Chen et al., 2017) （人像由This-Person-Does-Not-Exist生成）¶

图3.3.3 图像融合后门攻击 (Chen et al., 2017) （人像由This-Person-Does-Not-Exist生成）¶

基于全局随机噪声的后门攻击流程为：假定单个干净样本为\({\boldsymbol{x}}\)，其原始标签为\(y\)，目标后门标签为\(y_{t}\)，攻击的目标是使得后门模型将属于\(y\)的样本预测为\(y_{t}\)。具体策略为，定义一组干净样本\(\sum({\boldsymbol{x}})\)，对其中输入\({\boldsymbol{x}}\)施加噪声\(\boldsymbol{\delta}\)以便生成后门样本：

(3.3.2)¶\[\sum\nolimits^{rand}({\boldsymbol{x}})=\{\text{Clip}({\boldsymbol{x}}+\boldsymbol{\delta})|\boldsymbol{\delta} \in [-5, 5]^{H×W×3}\}\]

其中，\({\boldsymbol{x}}\)为输入的干净样本，\(H\)和\(W\)分别为高和宽，\(\text{Clip}(\cdot)\)函数将\({\boldsymbol{x}}\)限制到有效像素值（\([0, 255]\)）范围内。如图3.3.2 所示，攻击者利用\(\sum({\boldsymbol{x}})\)对\({\boldsymbol{x}}\)随机加入细微的噪声生成一组后门样本\({\boldsymbol{x}}_{p_1},{\boldsymbol{x}}_{p_2},\cdots,{\boldsymbol{x}}_{p_N}\)，同时将生成的样本类别重新标注为\(y_{t}\)并加入训练集。在该训练集上训练得到的后门模型会在测试阶段将任意后门样本\({\boldsymbol{x}}_{p}\)预测为类别\(y_{t}\)，以达到攻击目标。实验表明，这种攻击在较低的后门注入率下（比如5%）也能够达到将近100%的攻击成功率。

基于图像混合的后门攻击与上述基于全局噪声的攻击类似，不过后门触发器由随机噪声变成了某个特定的图像。具体地，假定后门触发背景图像为\(k\)，攻击者将触发器与部分干净训练样本按特定比例\(p\)融合构成后门样本，同时修改标签为\(y_{t}\)并加入训练集。具体定义如下：

(3.3.3)¶\[\prod\nolimits_\alpha^{blend}(k,{\boldsymbol{x}})=(1-\alpha)\cdot {\boldsymbol{x}} + \alpha\cdot k\]

其中，\({\boldsymbol{x}}\)为训练集中随机采样的要与触发器背景图像\(k\)融合的样本，\(\alpha\in [0,1]\)为控制融合的参数。当\(\alpha\)较小时，插入的触发器背景不易被人眼所察觉，具有较强的隐蔽性。上述的融合和覆盖策略保留了原始图片的部分像素，并将需要覆盖的像素值设置为背景图\(k\)与原始像素的融合值，如图3.3.3 所示。在通过这些策略生成一组后门样本后，将其标注为目标类别\(y_{t}\)并加入训练集。在该训练集上训练得到的模型会在测试时把任何融入了背景图\(k\)的样本预测为类别\(y_{t}\)。

至此，我们介绍了后门领域两种经典的脏标签攻击算法：BadNets和Blend。在接下来的章节中，我们将介绍一类更隐蔽的后门攻击方法：干净标签攻击，此类方法在不修改标签的情况下依然可以达到很高的成功率。

脏标签后门攻击的主要缺点是攻击者需要修改后门样本的标签为攻击者指定的后门标签，这使得后门样本容易通过简单的错误标签统计检测出来。净标签攻击只添加触发器不修改标签，可以避免修改标签所带来的隐蔽性问题。由于净标签攻击不修改标签，所以为了实现有效攻击就必须在后门类别的样本上添加触发器。举例来说，假设攻击者的攻击目标是第0类，那么净标签攻击只能对第0类的数据进行投毒，而非其他类别，这样才能在不影响模型功能的前提下完成攻击。此外，净标签攻击也往往需要额外的触发器增强手段来提升攻击强度。

干净标签后门攻击（Clean-Label Backdoor Attack，CLBA） (Turner et al., 2018) 是第一次提出干净标签后门概念的攻击方法。从思想上来说，CLBA攻击通过特定操作使待毒化样本的原始特征变得模糊或受到破坏，让模型无法从这些样本中获取有用的信息，转而去关注后门触发器特征。对原始图像的干扰操作可以分为两种：基于生成模型的插值和对抗扰动。生成模型诸如生成对抗网络（GAN）或变分自编码器（VAE）可以通过插值的方式改变生成数据的分布。攻击者可以利用生成模型的这一特点来将目标类别的样本转换为任意非目标类别的样本，这些样本所具有的原始特征被模糊化。在训练时，模型为了正确分类这些插值样本，则会去关注后门触发器。

给定生成器\(G:{\mathbb{R}}^d\longrightarrow {\mathbb{R}}^n\)，基于输入随机向量\({\boldsymbol{z}}\in {\mathbb{R}}^d\)生成维度为\(n\)的图像\(G({\boldsymbol{z}})\)。那么，对于目标图像\({\boldsymbol{x}}\in {\mathbb{R}}^n\)，定义编码函数为：

(3.3.4)¶\[E_G({\boldsymbol{x}})=\mathop{\mathrm{arg\,min}}\limits_{{\boldsymbol{z}}\in {\mathbb{R}}^d}{\lVert {\boldsymbol{x}}-G({\boldsymbol{z}}) \rVert}_2\]

基于此编码函数，对于给定插值常数\(\tau\)，定义插值函数为：

(3.3.5)¶\[I_G({\boldsymbol{x}}_1,{\boldsymbol{x}}_2,\tau)=G(\tau {\boldsymbol{z}}_1+(1-\tau){\boldsymbol{z}}_2), \, {\boldsymbol{z}}_1=E_G({\boldsymbol{x}}_1), \, {\boldsymbol{z}}_2=E_G({\boldsymbol{x}}_2)\]

其中，\({\boldsymbol{x}}_1\)与\({\boldsymbol{x}}_2\)分别为目标类别样本与任意非目标类别样本，\(I_G\)先将二者投影到编码空间得到向量\({\boldsymbol{z}}_1\)与\({\boldsymbol{z}}_2\)，随后通过插值常数\(\tau\)对\({\boldsymbol{z}}_1\)和\({\boldsymbol{z}}_2\)进行插值操作，最后再将得到的向量还原到输入空间，得到插值图像\({\boldsymbol{x}}_{GAN}\)。

另一种触发器增强策略是利用对抗扰动来阻止模型对原始特征的学习。在干净标签的设定下，后门触发器只能安插于目标类别的部分样本中，模型可能会只捕捉到干净特征而忽略了后门触发器。考虑到对抗噪声可以以高置信度误导模型，因此可以使用对抗噪声干扰模型的注意力，通过破坏干净特征使模型更容易捕获后门特征（如图3.3.4 所示）。对于给定输入\({\boldsymbol{x}}\)的对抗扰动操作定义如下：

(3.3.6)¶\[{\boldsymbol{x}}_{adv}=\mathop{\mathrm{arg\,max}}\limits_{{\lVert {\boldsymbol{x}}'-{\boldsymbol{x}} \rVert}_p\leq\epsilon}\mathcal{L}_{adv}(f({\boldsymbol{x}}'),y)\]

其中，\(\epsilon\)为对抗扰动大小的上界，\({\boldsymbol{x}}\)和\(y\)分别为原始样本和其标签。这里采用PGD攻击算法来生成对抗扰动，用来生成扰动的模型可以是独立对抗训练的鲁棒模型。

图3.3.4 对干净图像进行对抗扰动 (Turner et al., 2018)¶

上述两种方法都可以有效提高净标签后门攻击的成功率，二者中对抗扰动的增强效果更好。此外，提高插值常数\(\tau\)与对抗扰动上界\(\epsilon\)都可以对干净特征产生更大的干扰，进而提高后门攻击成功率，但是增加插值和扰动会降低后门样本的隐蔽性。因此，在实际应用中，攻击者需要在攻击成功率与隐蔽性之间进行权衡。

输入感知攻击 早期的后门攻击方法大都对整个数据集设计一个单一的触发器样式，然后向要投毒的样本中添加相同的触发器图案，并没有区分样本间的差异。输入感知后门攻击（Input-Aware Backdoor Attack，IABA） (Nguyen and Tran, 2020) 对不同投毒样本进行了区分。与早期后门攻击方法不同，输入感知攻击的触发器随输入样本而改变，即每个投毒样本都添加不同的触发器样式。输入感知攻击打破了触发器“输入无关”的传统假设，构建了触发器与输入相关的新型攻击思路。

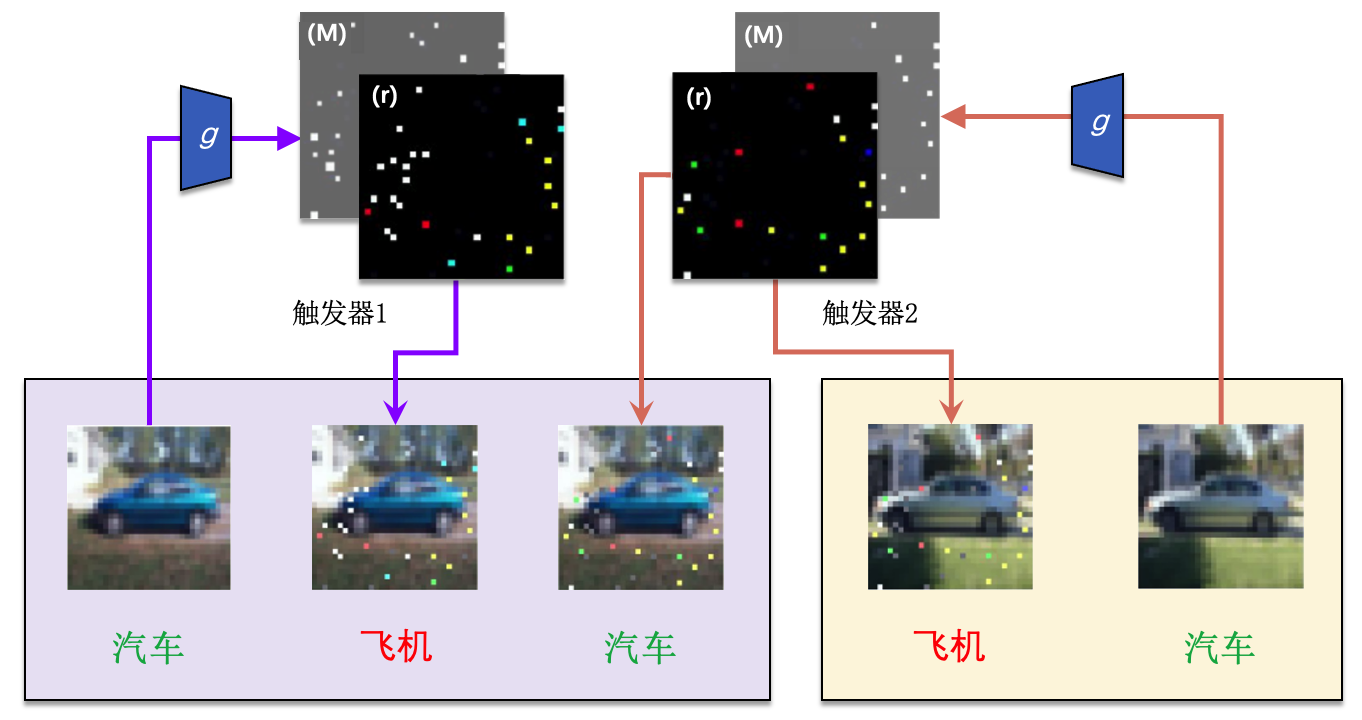
图3.3.5 输入感知攻击示意图 (Nguyen and Tran, 2020)¶

图3.3.5 展示了输入感知攻击的一般流程。攻击者使用生成器\(g\)根据输入图像创建触发器\((M,{\boldsymbol{r}})\)（\(M\)为图片掩码，\({\boldsymbol{r}}\)为触发器图案）。中毒的分类器可以正确地识别干净的输入(最左边和最右边的图像)，但在注入相应的触发器(第二和第四张图像)时返回预定义的标签(“飞机”)。“触发器-输入”是相互匹配的，向不匹配的干净图片中插入触发器并不会激活攻击(中间图像)。为了实现这一目标，研究者提出了多损失驱动的触发器生成器。该生成器采用了常规的编码器-解码器架构。假定训练模型为\(f: {\mathcal{X}} \rightarrow {\mathcal{Y}}\)，其中\({\mathcal{X}}\)是输入样本空间，\({\mathcal{Y}}=\{0, 1, \cdots, m-1\}\)为\(m\)个输出类别空间。后门触发函数定义为\(\mathcal{B}\)，则在干净样本上添加后门触发器\(t=({\boldsymbol{m}}, {\boldsymbol{r}})\)定义为:

(3.3.7)¶\[\mathcal{B}({\boldsymbol{x}},t) = {\boldsymbol{x}} \odot (1-{\boldsymbol{m}}) + {\boldsymbol{r}} \odot {\boldsymbol{m}}\]

其中，\({\boldsymbol{m}}\)表示触发器的掩码，用来控制触发器的稀疏性；\({\boldsymbol{r}}\)代表生成的触发器图案。

输入感知攻击的损失函数由两部分组成：分类损失和多样性损失。分类损失采用交叉熵损失\(\mathcal{L}_{CE}\)，以一定概率\(p\)为训练数据添加后门触发器以实现后门注入。多样性损失\(\mathcal{L}_{div}\)鼓励生成器生成多样化的触发器样式，在形式上避免重复，满足触发器和样本之间的对应关系。上述两个损失通过加权和组成总损失函数：

(3.3.8)¶\[\mathcal{L} = \mathcal{L}_{CE} + \lambda \mathcal{L}_{div}\]

输入感知攻击在触发器和样本上实现了关联性耦合，提供了一种更灵活的触发器生成模式。但是，这样的后门触发器也存在缺点。一方面，生成的触发器样式在视觉上是可察觉的，隐蔽性较差；另一方面，输入感知攻击仍然是一种脏标签攻击，需要修改后门样本的标签，这制约了其在现实场景中的威力。与输入感知攻击同期的工作，图像隐写后门攻击 (Li et al., 2021) 基于编码器-解码器将一个字符串（后门标签）隐写到图像中，从而可以在更高隐蔽性的情况下完成后门攻击，该攻击的触发器也会随输入样本的不同而发生变化，同时不需要修改投毒图像的类别（因为类别信息已经隐写到图像中了）。实验表明，该攻击能在大规模图像数据（如ImageNet数据集）上取得较高的攻击成功率。

3.3.2. 参数空间攻击¶

向模型中安插后门并不一定要以数据投毒的方式进行，还可以通过修改模型参数达到。参数空间攻击就是这样一类不依赖数据投毒的后门攻击。此类攻击利用逆向工程等技术，从预训练模型中生成后门触发器，并通过微调等形式将触发器植入模型。相较于输入空间后门攻击，参数空间后门攻击要求攻击者在不能访问原始训练数据的前提下，对给定模型实施后门攻击。下面介绍两个经典的参数空间后门攻击方法。

木马攻击 特洛伊木马攻击（Trojan attack） (Liu et al., 2018) ，简称为木马攻击，无疑是最经典的参数空间攻击方法。木马攻击的威胁模型很接近现实，因为在实际应用场景中，数据收集和模型训练等关键过程往往掌握在模型厂商的手里，这些过程需要耗费大量的资源，所以攻击者没有必要为了安插后门而花费高额的代价。但是，木马攻击允许攻击者直接对预训练完成的模型进行攻击，大大降低了攻击代价。简单来说，木马攻击的目标是在训练数据不可知且不可用的前提下，对已经训练好的模型实施攻击。

木马攻击的流程如图3.3.6 所示，大致分为三步：木马样式生成、训练数据生成和木马植入。下面将分别介绍这三个步骤所使用的方法。

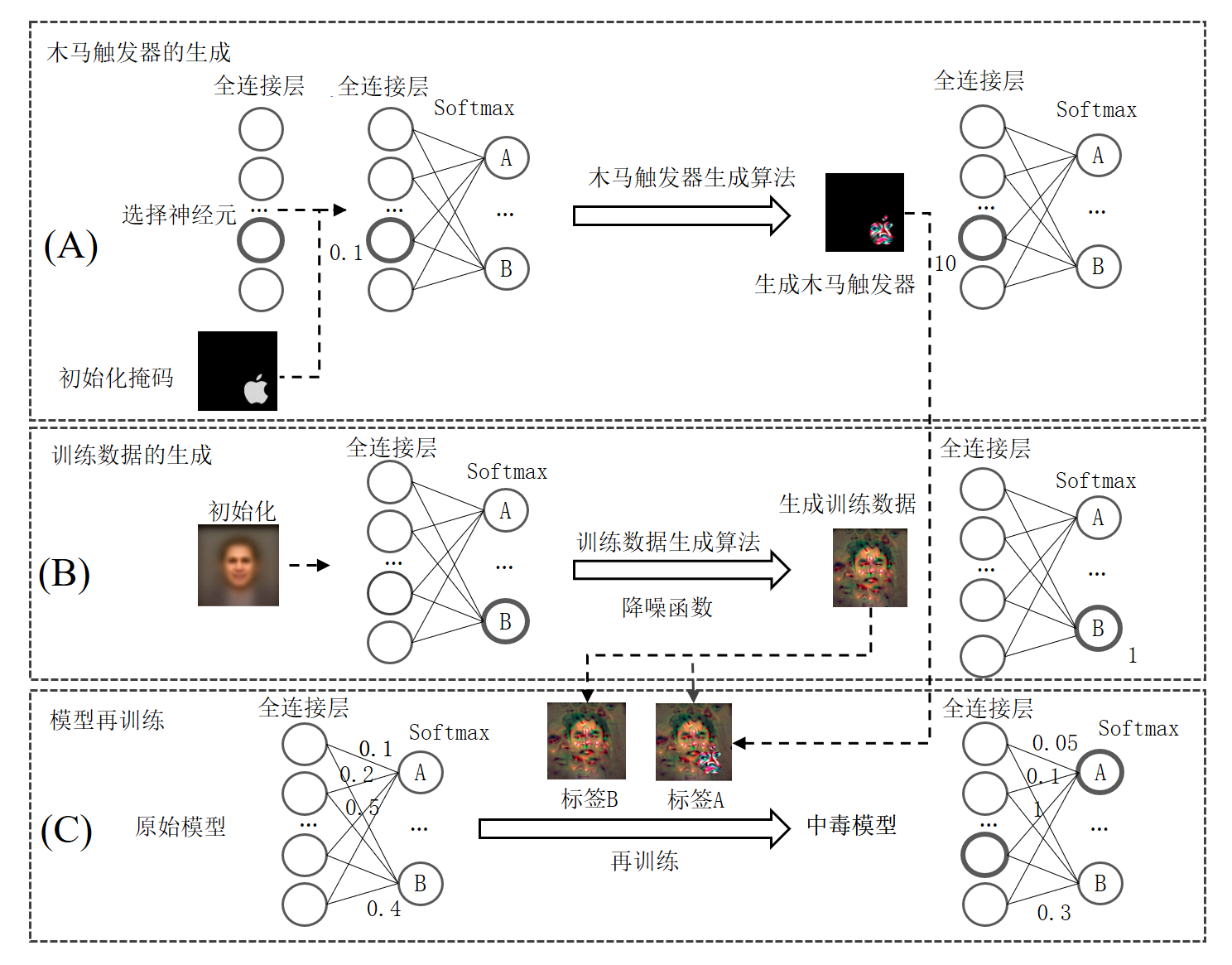
图3.3.6 木马攻击的基本流程 (Liu et al., 2018)¶

（1）木马样式生成：考虑到模型从输入中提取到的特征决定了其输出，因此所安插的木马需要与模型的关键神经元有很强的关联，才能改变模型的深层特征，进而导致其分类错误。因此，木马攻击选取模型某一层的一组特定神经元来生成后门触发器样式\({\boldsymbol{r}}\)。给定模型\(f\)在第\(l\)层的一组神经元与其对应的激活目标值\({(e_1, v_1), (e_2, v_2), \cdots }\)，木马样式\({\boldsymbol{r}}\)可以通过最小化下面的损失函数进行优化：

(3.3.9)¶\[\mathcal{L}_{trj}(f,{\boldsymbol{r}}) = (v_1-f_{e_1})^2 + (v_2-f_{e_2})^2 + \cdots\]

其中，梯度为\(\nabla=\frac{\partial \mathcal{L}_{trj}(f,{\boldsymbol{r}})}{\partial{\boldsymbol{r}}}\)，对\({\boldsymbol{r}}\)按一定步长\(\eta\)进行基于梯度下降的迭代更新\({\boldsymbol{r}}={\boldsymbol{r}}−\eta\cdot \nabla\)，直至收敛。最终得到的\({\boldsymbol{r}}\)即为生成的木马样式。上述优化过程在特定神经元与木马样式之间建立了强有力的关联，保证一旦出现对应的木马样式，这些神经元就会被显著激活，从而指向后门目标类别。

（2）训练数据的生成：由于攻击者并没有对原始训练数据的访问权限，因此需要利用逆向工程来生成部分训练数据作为后门植入的媒介。逆向工程的目的是将一张与原始数据集无关的图像\({\boldsymbol{x}}'\)，转化为能够代表原始数据集中类别为\(y_t\)的样本。\({\boldsymbol{x}}'\)可以是从不相关的公共数据集中随机抽取的一张图像或者是对大量随机不相关图像进行平均得到的平均图像。为了模仿原始训练数据，需要更新输入\({\boldsymbol{x}}'\)使其能够产生与原始训练样本相同的激活值。假定分类层中类别\(y_t\)的输出神经元激活为\(f_{y_t}\)，输入\({\boldsymbol{x}}'\)对应的目标值为\(v\)，数据逆向的损失函数定义为：

(3.3.10)¶\[\mathcal{L}_{rvs}(f, {\boldsymbol{x}}')=(v-f_{y_t}({\boldsymbol{x}}'))^2\]

与木马样式的生成过程类似，数据逆向利用输入层的梯度信息\(\nabla=\frac{\partial \mathcal{L}_{rvs}(f, {\boldsymbol{x}}')}{\partial {\boldsymbol{x}}'}\)，对\({\boldsymbol{x}}'\)按一定步长\(\eta\)进行迭代更新\({\boldsymbol{x}}'={\boldsymbol{x}}'−\eta\cdot \nabla\)，直到收敛。最终得到的\({\boldsymbol{x}}'\)即可作为原始训练数据类别\(y_t\)的替代数据。值得注意的是，这一过程需要遍历模型的所有输出类别，得到所有类别的替代数据。

（3）木马植入：在得到木马样式以及逆向数据集后，就可以对模型植入木马。具体地，对逆向数据集中的样本\({\boldsymbol{x}}'\)添加木马触发器\({\boldsymbol{r}}\)，同时修改它们的标签为后门标签\(y_t\)，得到包含“木马样本-后门标签”\(({\boldsymbol{x}}'+{\boldsymbol{r}},y_t)\)的木马数据集。在木马数据集上对干净模型进行微调，便可以将木马样式植入模型。微调可以在用于生成木马的那一层上进行，这样能极大地减少微调开销，同时保证攻击效果。

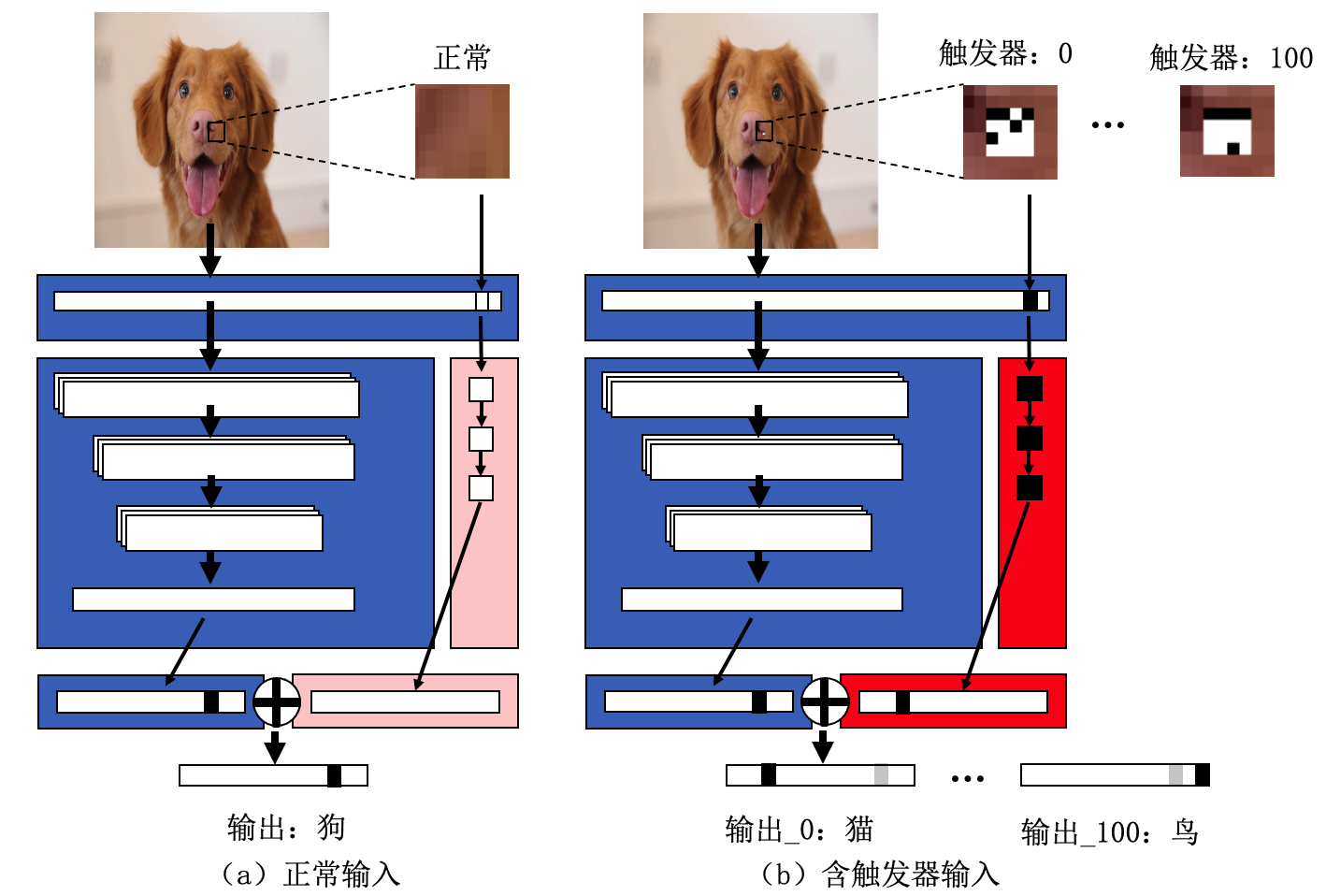
图3.3.7 TrojanNet攻击（粉色和红色部分为木马模块） (Liu et al., 2018)¶

TrojanNet攻击 后门攻击还可以直接对目标模型的结构进行调整，构建具有木马功能的模块，然后拼接到目标模型上去。此类攻击的思想跟输入空间攻击有一定的相似性，输入空间攻击通过数据投毒在干净数据的基础上增加额外的毒化数据，而结构攻击则是在干净模型的基础上增加额外的木马模块。此类方法的一个代表性工作是TrojanNet攻击 (Tang et al., 2020) 。TrojanNet的攻击流程如图3.3.7 所示，大致分为以下三个步骤：

（1）构造木马模块：攻击者需要事先定义木马数据，通常木马触发器为\(4\times4\)大小的二值化像素块。然后，定义一个多层感知机模块\(m\)，并在预先定义的木马数据上对\(m\)进行训练，得到木马模块\(m_t\)。为了保证木马模块\(m_t\)能够与目标模型架构匹配，需要根据目标模型的输出维度来调整木马模块的输出维度。

（2）木马模块与目标模型拼接：可以采用加权求和的方式对目标模型输出结果\(y_{c}\)和木马模块的输出结果\(y_{t}\)进行融合，定义如下：

(3.3.11)¶\[y=\mathrm{softmax}\left(\frac{\alpha y_{t}}{\tau}+\frac{(1-\alpha) y_{c}}{\tau}\right)\]

其中，\(\alpha \in (0.5,1)\)为融合权重，\(\tau\)为温度系数，用于调节模型输出的置信度。干净样本不会激活木马模块，所以预测结果\(y_{t}\)为全0，模型最终输出由\(y_{c}\)决定；一旦出现触发器图案，\(y_{t}\)将会主导模型的预测结果，迫使模型产生错误分类。

（3）引导输入特征传入木马模块：为了保证输入特征能够顺利地通过木马模块，作者构建了一个二值化掩码来保留图像中的木马区域，同时将其他区域像素值强制置为0。TrojanNet攻击的优势在于，一方面不需要接触到原始训练样本，另一方面木马模块隐式保留在目标模型架构中，具有较强的隐蔽性。

3.3.3. 特征空间攻击¶

这是后门攻击快速发展过程中衍生出来的一种新型攻击，这类攻击假设训练过程是可以操纵的，攻击者掌握训练数据、超参数、训练过程等几乎所有信息。大部分情况下，攻击者就是模型训练者（比如恶意的第三方训练平台或模型发布者）。这种攻击的兴起源于当前人工智能对第三方训练平台和预训练大模型的依赖。

隐藏触发器后门攻击 (Saha et al., 2020) （Hidden Trigger Backdoor Attack，HTBA）是一个有代表性的特征空间攻击算法，该攻击不仅保证了图像与标签的一致性（即干净标签设定），还保证了后门触发器的隐蔽性。与此前攻击不同，HTBA攻击基于目标和源样本在模型的特征空间优化生成后门样本。生成的后门样本在特征空间中与后门类别的干净样本具有相同的表征。HTBA的攻击流程如图3.3.8 所示，具体包含以下阶段：

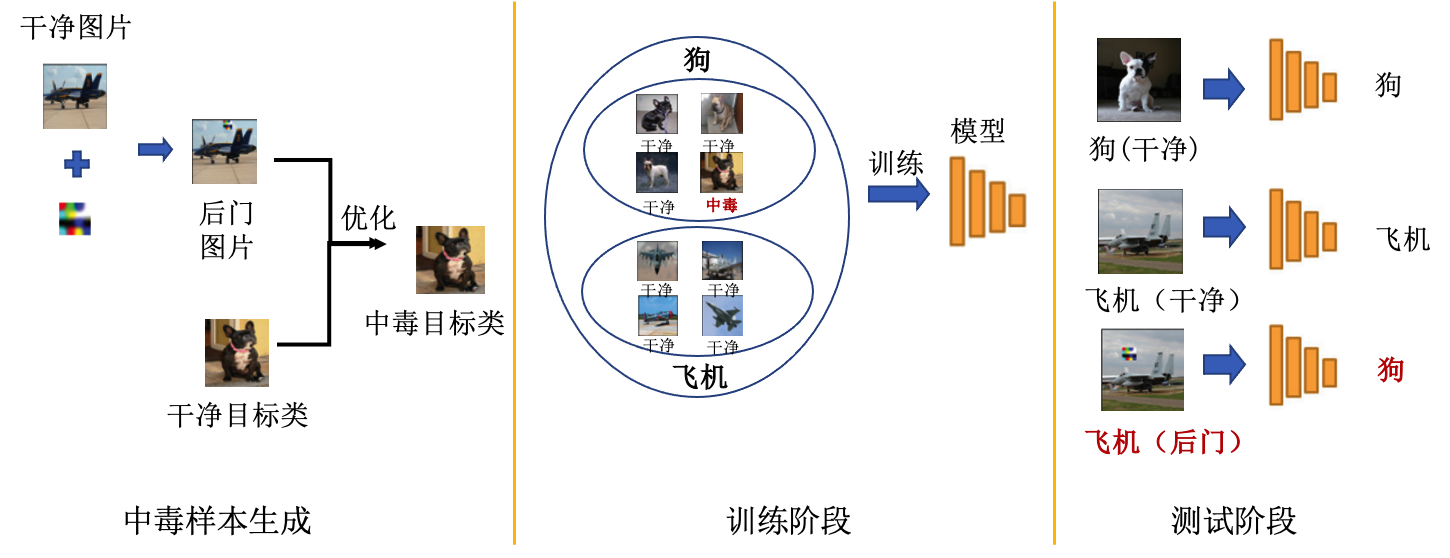
图3.3.8 隐藏后门攻击（HTBA）流程 (Saha et al., 2020)¶

（1）构建干净参考模型：为了实现后门样本和干净样本在特征空间上的相似性，首先需要在干净数据集上训练一个良性参考模型\(f\)，作为受害者模型。攻击者需要利用良性参考模型来帮助攻击者在特征空间里生成能够指向攻击目标的后门样本。

（2）后门触发优化：给定源样本\({\boldsymbol{x}}_s\)和目标样本\({\boldsymbol{x}}_t\)，定义后门触发器为\({\boldsymbol{r}}\)，则显式后门样本表示为\(({\boldsymbol{x}}_s+{\boldsymbol{r}})\)。可以借助一个额外的样本\({\boldsymbol{x}}_b\)将显式后门样本隐藏成隐式后门样本，对应的优化问题如下：

(3.3.12)¶\[\begin{split}\begin{aligned}& \mathop{\mathrm{arg\,min}}\limits_{{\boldsymbol{x}}_b}{\lVert f({\boldsymbol{x}}_b)-f({\boldsymbol{x}}_s+{\boldsymbol{r}}) \rVert}^2_2 \\& s.t. \;\; \left\|{\boldsymbol{x}}_b-{\boldsymbol{x}}_t\right\|_\infty<\epsilon\end{aligned}\end{split}\]

其中，\(f(\cdot)\)表示干净模型的深层特征输出，\({\boldsymbol{x}}_b\)为优化得到的后门样本。上面隐藏触发器的优化过程，一方面保证了隐式后门样本\({\boldsymbol{x}}_b\)在功能上具有与显式后门样本\({\boldsymbol{x}}_s+{\boldsymbol{r}}\)一样的触发效果；另一方面，由于\(\epsilon\)的限制，\({\boldsymbol{x}}_b\)在输入空间中与目标类别样本\({\boldsymbol{x}}_t\)非常接近，保证了输入空间中后门触发器的隐蔽性。此外，在迭代过程中使用不同的源样本可以进一步提高攻击的隐蔽性和泛化性。

3.3.4. 迁移学习攻击¶

迁移学习（transfer learning）旨在将某个领域或任务上学习到的知识迁移应用到其他相关领域中，避免了每次在新领域都需要从头训练模型的应用难题。常用的微调技术即是迁移学习的一种。以深度模型为例，用户可以通过开源平台下载预训练模型权重，然后利用本地数据对预训练模型进行微调，从而使其适配本地下游任务。迁移学习极大地缩短了训练模型的时间和计算成本，在当今人工智能中扮演着重要的角色。

迁移学习可以被认为涉及两种模型，分别是作为教师模型的预训练模型和作为学生模型的下游任务模型。教师模型通常指由大型公司或机构完成，并在相关平台上进行发布，以供其他用户下载使用的大模型；而学生模型指用户针对自己本地特定任务，基于教师模型进行微调得到的小模型。

图3.3.9 展示了迁移学习的一般流程。具体而言，模型微调首先利用教师模型对学生模型进行初始化。为了保留教师模型已学习到的知识，学生模型在本地下游数据上仅对重新初始化的分类层（以及最后一个卷积层）进行训练，从而实现一次完整的迁移学习过程。相较于从零开始训练学生模型，迁移学习可以节省大量的计算开销，且在一定程度上提高学生模型的泛化性能。

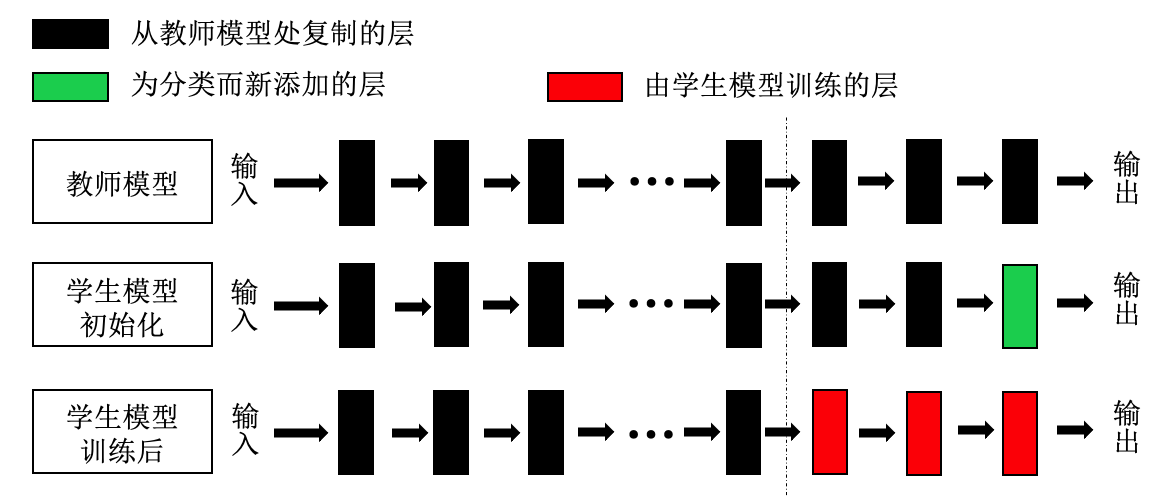
图3.3.9 迁移学习示意图 (Yao et al., 2019)¶

潜在后门攻击（Latent Backdoor Attack，LBA） (Yao et al., 2019) 即是一个专门针对迁移学习提出的后门攻击方法。攻击者预先在教师模型中安插特定的后门样式，将其与后门类别关联，在此教师模型上微调得到的学生模型就会继承教师模型中的后门。潜在后门攻击的流程如图3.3.10 所示，主要有以下四个步骤：

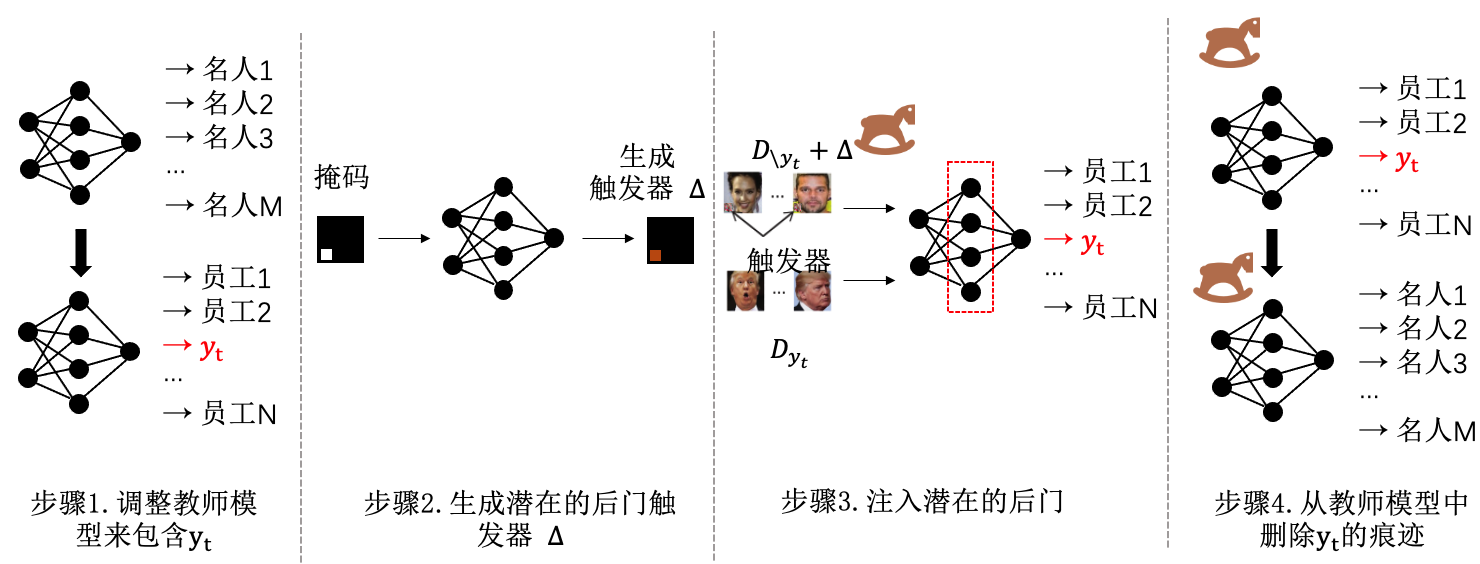
图3.3.10 潜在后门攻击流程 (Yao et al., 2019)¶

（1）将后门类别植入教师模型：给定一个训练完成的教师模型，首先需要将攻击目标类别\(y_t\)嵌入教师中。为此可以构造两个数据集\(D_{y_t}\)和\(D_{\backslash y_t}\)。其中\(D_{y_t}\)为一组目标类别的干净样本，\(D_{\backslash y_t}\)为一组非目标类别的干净样本，攻击者在这两组数据上微调教师模型的分类层，将使教师模型的参数关联至攻击目标类别\(y_t\)。

（2）生成潜在后门触发器：对于给定后门位置与形状，攻击者需要根据教师模型的特征层信息，迭代优化生成潜在后门触发器。具体地，选定特征层\(L_t\)，\(f^{L_t}\)表示老师模型在层\(L_t\)提取到的特征，则触发器样式\({\boldsymbol{r}}\)可以通过解下列优化问题获得：

(3.3.13)¶\[\mathop{\mathrm{arg\,min}}\limits_{{\boldsymbol{r}}}\sum_{{\boldsymbol{x}}\in D_{\backslash y_t}\cup D_{y_t}}\sum_{{\boldsymbol{x}}_t\in D_{y_t}}{\lVert (f^{L_t}({\boldsymbol{x}}+{\boldsymbol{r}}),f^{L_t}({\boldsymbol{x}}_t) \rVert}^2_2\]

上述优化的目标是使后门样本\({\boldsymbol{x}}+{\boldsymbol{r}}\)在特征空间中与目标类别的样本具有相似的特征表示，从而加强后门触发器与目标类别之间的关联，提升攻击成功率。

（3）后门触发器植入：该步骤将生成的潜在后门触发器植入到教师模型中。具体地，指定教师模型的特征层\(L_t\)，\(\overline{f^{L_t}_{y_t}}\)为在特征空间中表征目标类别\(y_t\)的所有样本的中心点。后门植入的优化过程定义为：

(3.3.14)¶\[\mathcal{L}({\boldsymbol{x}},y,y_t)=\mathcal{L}_{CE}(y,f({\boldsymbol{x}}))+\lambda\cdot {\lvert {f^{L_t}({\boldsymbol{x}}+{\boldsymbol{r}}),\overline{f^{L_t}_{y_t}}} \rVert}^2_2\]

总体损失函数包含两项，第一项为标准的模型训练损失(交叉熵)，第二项在特征空间中将后门样本映射到目标类别的特征中心点，\(\lambda\)为平衡二者的超参。

（4）移除目标类别:math:`y_t`：为了进一步提升潜在后门的隐蔽性，这一步直接移除后门教师模型的原始分类层，并重新初始化。该步骤削弱了后门在全连接层的输出显著性，提升了教师模型中后门输出特征的隐蔽性。

经过上述四个步骤，便完成了对教师模型的后门投毒。实验表明，潜在后门攻击能够在迁移学习的场景下取得很好的攻击效果。与此同时，考虑到被污染的教师模型中移除了目标类别的相关信息，因此用户很难察觉后门攻击的存在。

鲁棒迁移攻击 虽然潜在后门攻击显式地隐藏了后门特征和关联标签的信息，但是防御者依然可以通过观测教师模型中神经元的激活状态，判断当前模型是否已被安插后门。为了进一步提升后门相关神经元在迁移学习中的隐蔽性和一致性，鲁棒迁移攻击 (Wang et al., 2020) 利用自编码器构造更加鲁棒的迁移学习后门攻击。该攻击主要分为三个步骤：

（1）特定神经元选取：考虑到神经元激活值过低容易被剪枝防御所移除，而过高则容易在微调过程中改变原始权重，因此所选取的神经元的激活值应该在特定范围内。具体地，研究者按照神经元的激活绝对值对神经元进行从小到大移除。在移除过程中，当模型准确率在阈值范围\([\alpha_1,\alpha_2]\)之间时，移除神经元，当准确率低于\(\alpha_2\)后则停止移除。

（2）后门触发器生成：由于后门样本与干净样本具有不同的数据分布，因此，在干净数据上训练的自编码器可能无法生成隐蔽的后门触发器。为了使后门触发器具备隐蔽性，同时抵御激活裁剪等防御方法，研究者设计了如下优化函数来生成后门样式：

(3.3.15)¶\[\mathcal{L}=\lambda_1\sum_{j}(v_j-f_j({\boldsymbol{x}}+{\boldsymbol{r}}))^2+\lambda_2\sum_{{\boldsymbol{x}}_i\in T}{\lVert {\mathcal{A}}({\boldsymbol{x}}_i+{\boldsymbol{r}})-{\mathcal{A}}({\boldsymbol{x}}_i) \rVert}^2\]

其中，\({\boldsymbol{x}}\)为训练样本，\({\boldsymbol{r}}\)为待优化的后门样式。该函数包含两项：在第一个损失项中，\(v_j\)与\(f_j(\cdot)\)分别表示被选中神经元激活值的目标值与当前值，该项是为了让后门触发模式下的神经元激活与指定的神经元激活更加相似，从而提高后门攻击的成功率；在第二项中，\({\mathcal{A}}\)表示在公共数据集上训练得到的自编码器，该项的目的是缩小重构的后门样本与干净样本之间的距离，从而保证后门样本和干净样本的不可区分性，提高攻击的隐蔽性。

（3）后门植入：此步通过后门样本和干净样本微调特定神经元，建立攻击目标类别与被选中神经元的关联，实现后门触发器植入。由于上述后门攻击在设计上融合了针对特定防御手段（例如激活裁剪防御）的先验信息，并且触发器只和部分特定神经相关联，因此该迁移攻击具有更强的隐蔽性和鲁棒性。

3.3.5. 联邦后门攻击¶

基本的联邦学习包含\(n\)个参与者和负责更新全局模型\(g\)的中央服务器。在第\(t\)轮迭代时，服务器选取\(m\)个参与者并向其传递当前的全局模型\(g^t\)，每个被选中的参与者将在本地利用自己的数据在\(g^t\)的基础上（即用\(g^t\)的参数初始化）训练一个本地模型\(f^{t+1}\)，随后将差值\(f^{t+1}-g^t\)上传给服务器，服务器在接收这些信息后，利用如下FedAvg算法对全局模型进行更新：

(3.3.16)¶\[g^{t+1}=g^t+\frac{\eta}{n}\sum_{i=1}^m(f_i^{t+1}-g^t)\]

其中，\(\eta\)决定了每轮迭代中参与者对全局模型的贡献程度。经过多轮迭代至全局模型收敛，便完成了一次联邦学习。

联邦学习的后门攻击相比传统后门攻击相比更容易成功且更难防御。首先，为了确保全局模型的性能，联邦参与者数量往往非常庞大，难以避免参与者中存在恶意攻击者的可能性，所以攻击更容易成功、更隐蔽。其次，由于每个参与者都是受保护的，所以一些传统的后门防御方法（如后门样本检测）无法用来防御联邦后门攻击。这使得恶意攻击者可以轻易通过上传有毒梯度信息来污染全局模型，导致在联邦学习结束后所有参与者拿到的都是一个具有后门的全局模型。

由于联邦学习的特性，传统针对集中式模型训练的后门攻击算法不适用于联邦学习，目前研究学者提出的针对联邦学习的代表性后门攻击方法主要有三种：模型替换攻击、分布式后门攻击和边界后门攻击。

模型替换攻击（Model Replacement） (Bagdasaryan et al., 2020) 在本地训练一个后门模型并将模型参数上传，这是一种最直接、简单的联邦学习后门攻击方法。该攻击的攻击思路如图3.3.11 所示，假设攻击者能且只能对自己的本地数据与本地训练进行操作。此外，为了避免本地的恶意信息被其他干净模型平均，攻击者对所上传的差值信息进行了一定程度的放大。攻击者将要上传的本地模型设置为：

(3.3.17)¶\[\tilde{f}_{i}^{t+1}=\gamma(f_{i}^{t+1}-g^t)+g^t\]

其中，\(\gamma\)为缩放量。若令\(\gamma=\frac{n}{\eta}\)，那么将式 (3.3.16) 中本地模型\(f_i^{t+1}\)替换为放大后的有毒模型\(\tilde{f}_{i}^{t+1}\)，就可以把全局模型\(g^{t+1}\)替换为攻击者训练的后门模型\(f_i^{t+1}\)，而且还可以防止上传的模型被其他参与者模型中和。

如果攻击者无法了解服务器中的\(\eta\)与\(n\)等超参信息，则可以逐渐增大式 (3.3.17) 中本地的\(\gamma\)值，利用全局模型在后门数据上的准确率来对服务器中的超参信息进行估计与推算。另外，在放大更新信息的同时，攻击者还可以通过降低本地模型的学习率来保证当前被替换掉的全局模型中所安插的后门信息在后续的迭代过程中难以被遗忘。

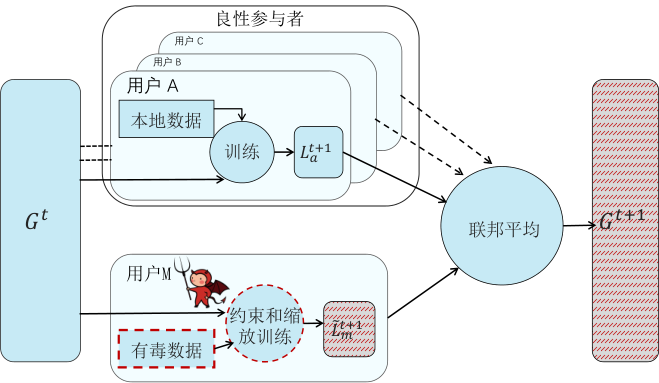
图3.3.11 基于模型替换的联邦学习后门攻击 (Bagdasaryan et al., 2020)¶

分布式后门攻击 传统后门攻击采用全局统一的后门样式，如果能将后门样式拆分成多个部分，利用分布式的思想进行联合攻击，便可以提高后门攻击的隐蔽性，而且还能充分利用联邦学习的分布式特性。分布式后门攻击（Distributed Backdoor Attack, DBA） (Xie et al., 2019) 便是基于此思想的一种攻击方法。如图3.3.12 所示，分布式后门攻击将后门触发器拆分给不同的参与者，每个参与者各自训练本地后门模型并上传至服务器。在测试阶段，可以用拆分前的完整触发器来攻击全局模型。

分布式后门攻击主要有以下两个关键点：

（1）确定影响触发的因素：在分布式后门攻击中，需要充分考虑后门样式的位置、大小、子后门样式之间的距离、污染比例等因素对攻击成功率的影响。

（2）投毒方式：对于任意一个恶意客户端，分布式后门攻击将全局触发器拆分为\(M\)个子触发器，然后在训练过程中依次将这些子触发器注入到不同的本地模型中，并最终达到对全局模型的持续性、累加式攻击目标。

相较于集中式后门攻击，分布式后门攻击能够获得更加持久的后门攻击效果。同时，由于全局触发器被拆分为多个更小的子触发器，进一步提升了攻击的隐蔽性。

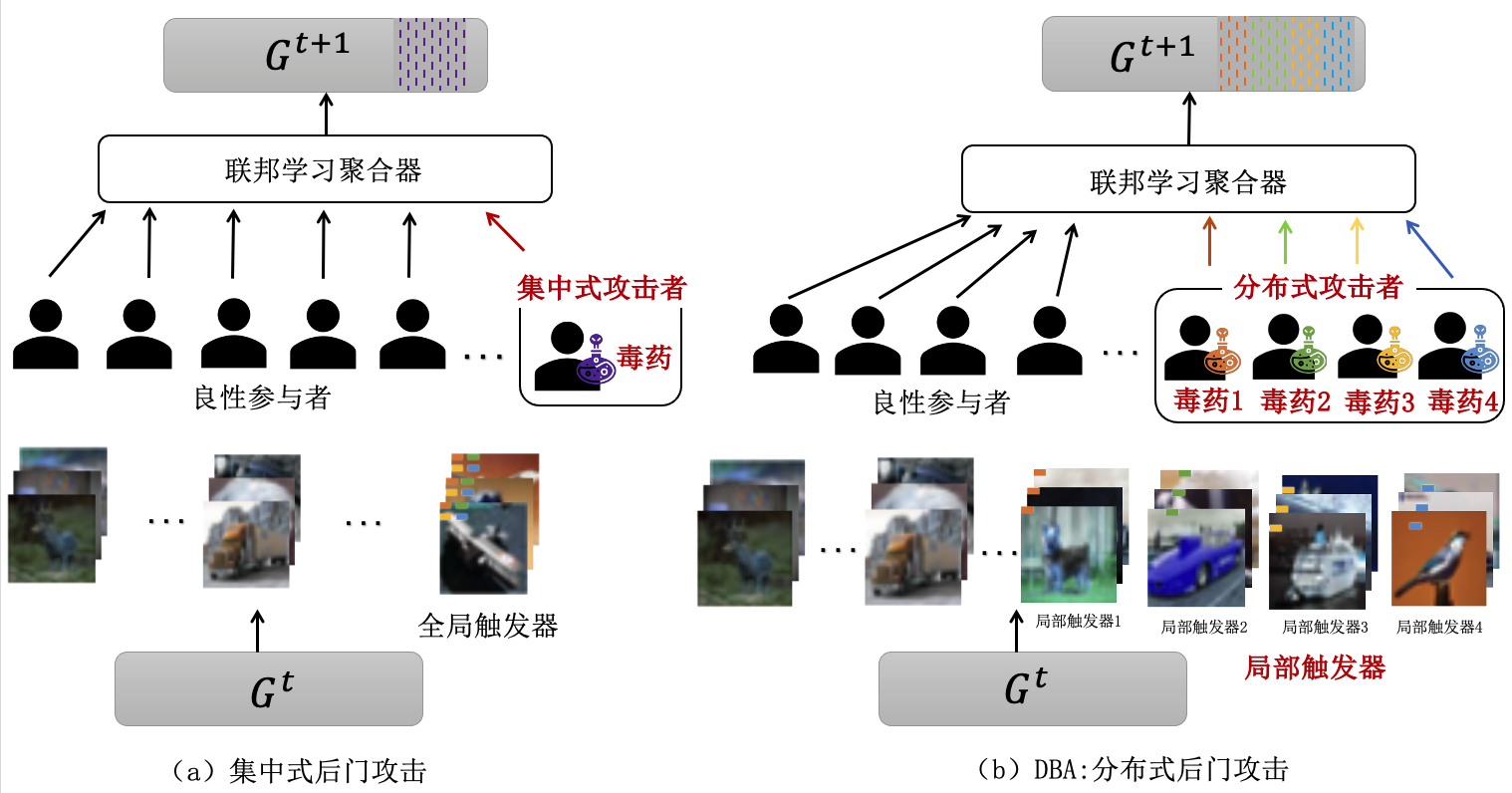
图3.3.12 集中式后门攻击与分布式后门攻击 (Wang et al., 2020)¶

边界后门攻击 研究发现，边界样本（edge examples）通常位于整个输入数据分布的尾部，出现频率较低，且通常不被用作训练或测试数据。与主要的数据类别相比，边界样本的占比很小，因此可以被用来设计隐蔽高效的投毒和后门攻击，而且在攻击的过程中不容易对其他主要类别的分类精度产生明显影响。具体地，基于边界样本的边界后门攻击（Edge-case Backdoors） (Wang et al., 2020) 主要包含两个步骤：

（1）构造边界样本集：假定边界数据集为\(D_{edge}=\{({\boldsymbol{x}}_i, y_t)\}\)，其中，边界数据\({\boldsymbol{x}}_i\)的采样概率满足\(P({\boldsymbol{x}}_i) \leq p\)；而\(y_t\)表示攻击者选定的目标类别。为了构造合适的边界数据集，需要确定给定数据的出现概率\(p\)。这一结果可以通过本地模型的分类层输出向量拟合一个高斯混合模型测量获得。最后，根据当前样本的给定概率是否小于\(p\)对数据进行过滤得到\(D_{edge}\)。

（2）后门注入：攻击者遵循普通训练流程，将构造完成的恶意边界数据添加到训练数据集中得到\(D^{'}=D\cup D_{edge}\)，并在此数据上训练局部模型，最终通过参数聚合污染全局模型。

实验表明，基于边界数据集的后门攻击具有较好的攻击性能和持续时间，且能有效规避裁剪、随机噪声等防御方法。然而，边界攻击的缺点在于边界数据的选择具有特殊性，即只能选取小概率出现的数据作为后门样本，而小概率样本很难收集。

3.4. 模型抽取¶

模型抽取 1 （Model Extraction）的攻击目标是抽取目标模型（也称受害者模型）的功能和性能。一般来说，模型抽取攻击的主要目标是实现对受害者模型低成本、高回报和低风险的抽取。其通过某种方法获得一个与受害者模型在功能和性能上都相近的替代模型，从而规避昂贵的模型训练成本，获得不当利益。模型抽取行为会严重侵犯人工智能知识产权。实际上，对人工智能知识产权的侵犯不只有模型抽取，未经授权的模型复制、微调、迁移学习（微调修改+微调）、水印去除等也都属于知识产权侵犯行为。这些潜在的风险给模型服务商带来了额外的挑战，要求他们不仅要满足用户的服务请求，还要有能力防御恶意的抽取行为，防止模型泄露。

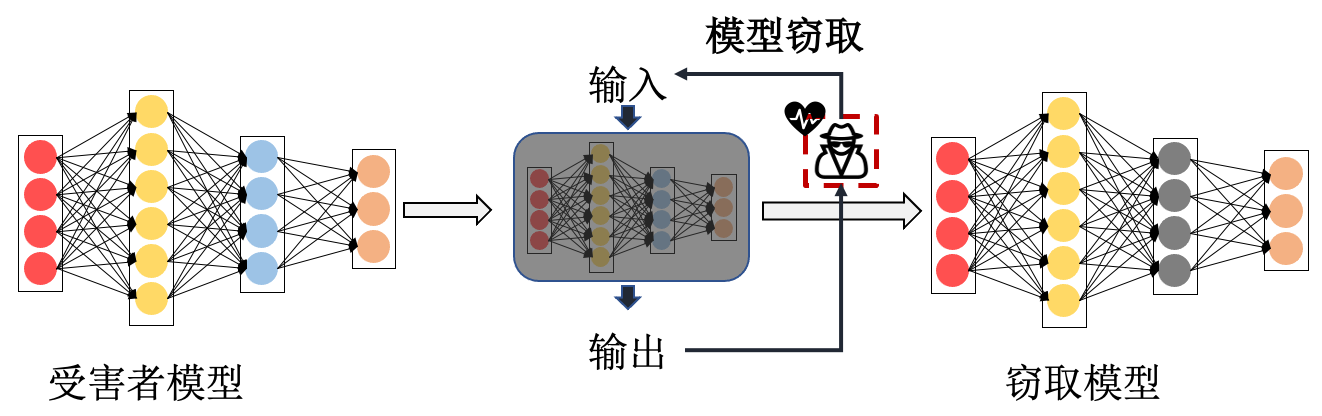
图3.4.1 模型抽取攻击示意图¶

如图3.4.1 所示，模型抽取攻击需要在与受害者模型交互查询访问的过程中完成。具体来说，攻击者通过有限次数访问受害者模型的黑盒API，输入不同的查询样本，这些样本可以是收集到的自然样本，也可以是合成的样本。之后查询受害者模型获得对应的预测输出，攻击者还可以通过观察预测输出的分布来调整自己的查询样本，以获取更多的受害者模型信息。在这个交互过程中，攻击者通过模仿学习获得一个与受害者模型相似的抽取模型，或者直接抽取受害者模型的参数以及超参数等关键信息。根据抽取目标和方式的不同，现有的抽取攻击可以大致分为一下三类：基于方程式求解的抽取攻击、基于替代模型的抽取攻击和基于元模型的抽取攻击。

3.4.1. 基于方程式求解的攻击¶

基于方程式求解的攻击（Equation-Solving Based Attack，ESBA） (Tramèr et al., 2016) 通过构建并求解受害者模型所表示的方程式来完成模型抽取。具体地，攻击者\(A\)根据受害者模型\(f\)的相关信息构建方程式，并利用特定输入\({\boldsymbol{x}}\)和受害者模型对应的输出\(f(\mathbf{x})\)（预测概率向量）来求解方程，从而获取与受害者模型相似的模型参数（即替代模型\(f'\)）。图3.4.2 展示了此类攻击的一般流程。

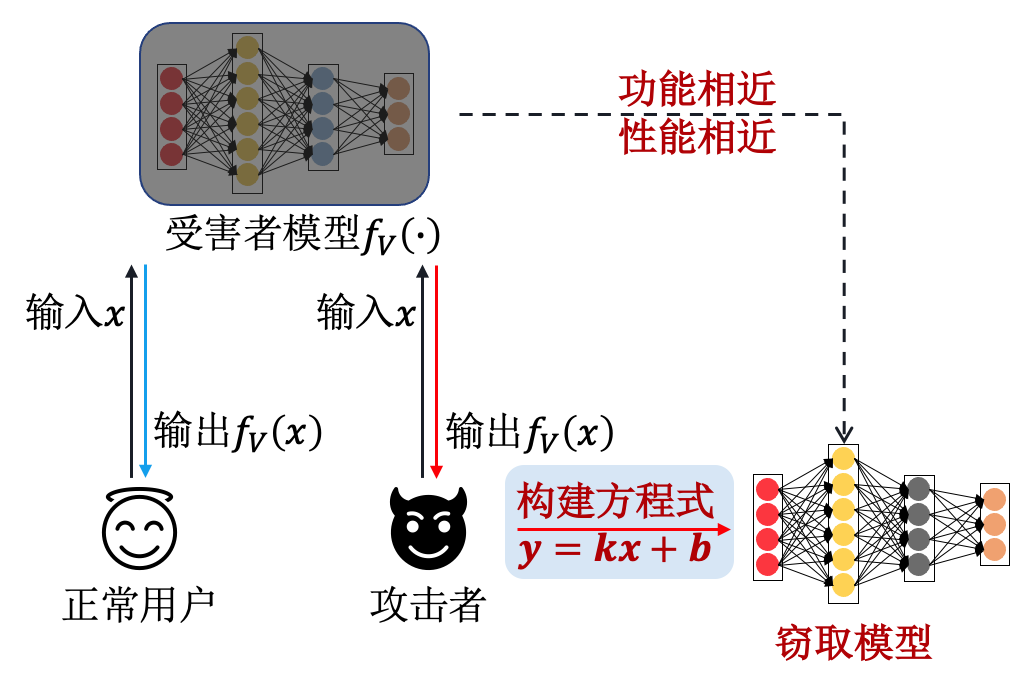
图3.4.2 基于方程式求解的模型抽取攻击流程图¶

可以证明，如果受害者模型具有\(d\)个参数，那么最少\(d+1\)个查询样本就可以求解模型参数\(\theta\)的方程式。以逻辑回归模型为例，可构建如下所示的线性方程：

(3.4.1)¶\[\begin{aligned}\theta^{\top}{\boldsymbol{x}}=\sigma^{-1}(f({\boldsymbol{x}}))\end{aligned}\]

其中，\(\theta\in\mathbb{R}^d\)为受害者模型参数，\(\sigma(t)=1/(1+e^{-t})\)为sigmoid激活函数，\(f({\boldsymbol{x}})=\sigma(\theta^{\top}{\boldsymbol{x}})\)为受害者模型的输出。通过多个“输入-输出”对，带入式 (3.4.1) 构建方程式组，求解之后得到受害者模型参数\(\theta\in\mathbb{R}^d\)。

除了模型自身参数，它的超参数同样具有重要意义，因为很多时候调参的代价远高于单次模型训练的代价，因而也面临着被抽取的风险。研究表明，在训练集和模型已知的情况下，攻击者可以准确抽取算法的超参数 (Wang and Gong, 2018) 。具体来说，受害者模型参数往往对应的是损失函数\(\mathcal{L}(\theta)=\mathcal{L}({\boldsymbol{x}},y,\theta)+\lambda R(\theta)\)的最小值，此时损失函数的梯度应为零（虽然实际情况下并非如此）。那么便可以列出如下和超参数\(\lambda\)相关的方程：

(3.4.2)¶\[\begin{aligned}\frac{\partial \mathcal{L}(\theta)}{\partial \theta} = {\boldsymbol{b}} + \lambda {\boldsymbol{a}} = 0\end{aligned}\]

(3.4.3)¶\[\begin{split}{\boldsymbol{b}}=\begin{bmatrix}\frac{\partial \mathcal{L}({\boldsymbol{x}},y,\theta)}{\partial \theta_1} \\\frac{\partial \mathcal{L}({\boldsymbol{x}},y,\theta)}{\partial \theta_2} \\\vdots \\\frac{\partial \mathcal{L}({\boldsymbol{x}},y,\theta)}{\partial \theta_n} \\\end{bmatrix}, \; {\boldsymbol{a}}=\begin{bmatrix}\frac{\partial R(\theta)}{\partial \theta_1} \\\frac{\partial R(\theta)}{\partial \theta_2} \\\vdots \\\frac{\partial R(\theta)}{\partial \theta_n} \\\end{bmatrix}\end{split}\]

其中，训练数据集\(D=\{{\boldsymbol{x}},y\}_{i=1}^{n}\)，模型参数\(\theta\)，正则项\(R\)，均为已知。故可通过最小二乘法求解超参数\(\lambda\)的方程式：

(3.4.4)¶\[\begin{aligned}\hat{\lambda}=-({\boldsymbol{a}}^{\top}{\boldsymbol{a}})^{-1}{\boldsymbol{a}}^{\top}{\boldsymbol{b}}\end{aligned}\]

该攻击将超参数、模型参数和训练数据集之间的关系构建成方程式，并证明了机器学习算法的超参数同样也可以被抽取。

可以看到，基于方程式求解的模型抽取攻击随着受害者模型参数量的增多，需要的查询样本和构建求解方程式的数量也都会增多。因此，这种攻击方式是一种针对传统机器学习模型的抽取攻击，只适用于逻辑回归、多层感知机、支持向量机和决策树等简单的机器学习模型，并不适用于复杂且参数众多的深度神经网络。

3.4.2. 基于替代模型的抽取¶

基于替代模型的抽取（Surrogate-Model Based Attack，SMBA）通过调用受害者模型来打标签，然后在打标签后的数据集上训练一个替代模型来近似受害者模型。具体地，攻击者\(A\)在不知道受害者模型\(f(\cdot)\)任何先验知识的情况下，向受害者模型的API输入查询样本\({\boldsymbol{x}}\)，获取受害者模型的预测输出\(f({\boldsymbol{x}})\)。随后，攻击者根据输入和输出的特定关系构建替代训练数据集\(D'=\{({\boldsymbol{x}},f({\boldsymbol{x}}))\}_{i=1}^{m}\)。通过在替代数据集\(D'\)上进行多次训练，攻击者就可以得到一个与受害者模型\(f(\cdot)\)在功能和性质上相近的替代模型\(f'(\cdot)\)，从而完成模型抽取攻击。图3.4.3 展示了该攻击的流程。

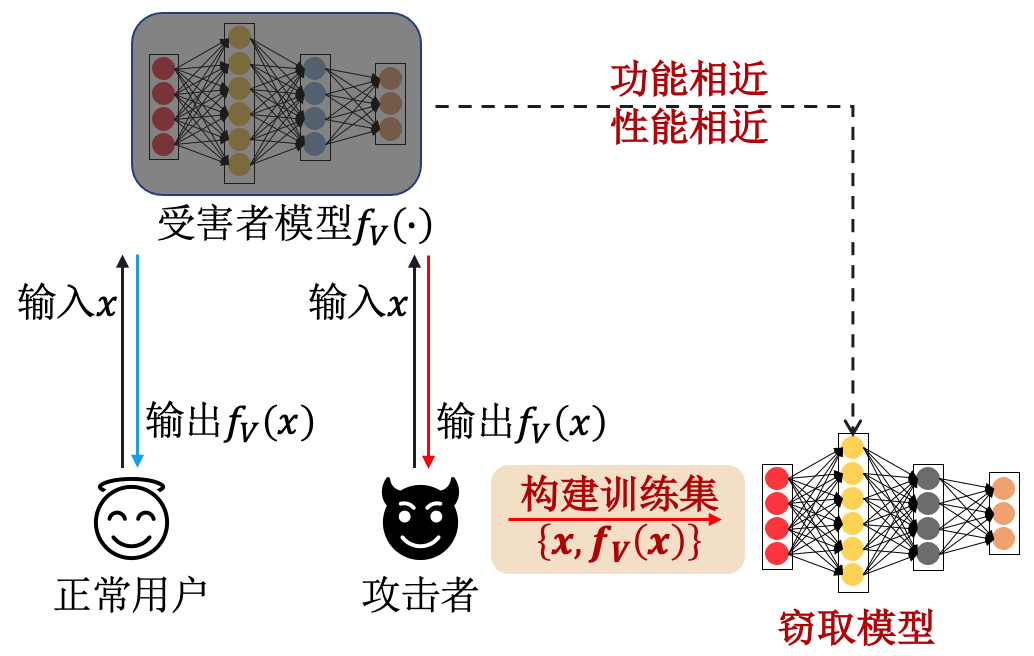
图3.4.3 基于替代模型的模型抽取流程¶

不难发现，模型抽取与知识蒸馏的过程很相似，但并不完全相同。这里给出二者的损失函数：

(3.4.5)¶\[\begin{split}\begin{aligned}& \mathcal{L}_{KD} = \lambda_{1} \mathcal{L}_{CE}(y,f_{S}({\boldsymbol{x}})) + \lambda_{2} \mathcal{L}_{CE}(f_{T}^{\tau}({\boldsymbol{x}}),f_{S}^{\tau}({\boldsymbol{x}})) \\& \mathcal{L}_{ME} = \mathcal{L}_{CE}(f({\boldsymbol{x}}),f'({\boldsymbol{x}}))\end{aligned}\end{split}\]

其中，\(\mathcal{L}_{KD}\)为知识蒸馏损失，\(\mathcal{L}_{ME}\)为模型抽取损失，\(y\)为真实标签（硬标签），\(f_{T}({\boldsymbol{x}})\)和\(f_{S}({\boldsymbol{x}})\)分别为教师模型和学生模型的概率输出（软标签），\(\tau\)为温度超参，\(f({\boldsymbol{x}})\)和\(f'({\boldsymbol{x}})\)分别为受害者模型和替代模型的预测输出。知识蒸馏中使用的样本\({\boldsymbol{x}}\)往往为教师模型的训练样本或来自相同分布的样本；而模型抽取中使用的样本\({\boldsymbol{x}}\)为攻击者收集或者合成的样本，可能偏离受害者模型原训练数据分布。可以看出，知识蒸馏的目的是将教师模型学到的特征蒸馏到学生模型中，而模型抽取的目的是重建一个与受害者模型一样的替代模型。

此外，模型抽取与黑盒对抗攻击也有一定的相似之处。黑盒对抗攻击通过查询目标模型、使用替代模型等方式，去近似目标模型的决策边界，从而生成具有高迁移性（从替代模型到目标模型）的对抗样本。而模型抽取则是通过类似的技术来估计目标模型的输出分布，以获取从输入到输出的映射函数（即目标模型所代表的决策函数），从而达到模型参数抽取的目的。

实际上，模型抽取可以和黑盒对抗攻击结合，产生更强的对抗攻击方法 (Papernot et al., 2017) 。该攻击首先使用抽取技术得到一个近似受害者模型决策边界的替代模型，然后基于替代模型生成对抗样本，再放过来利用对抗样本的迁移性攻击受害者模型。具体而言，攻击者先收集能够代表受害者模型输入分布的少量数据，然后通过查询受害者模型的预测输出构建替代模型的替代训练集，该数据集能够较好地刻画受害者模型的决策边界。之后可以利用替代训练集训练得到替代模型。替代训练集还可以通过数据合成技术进行扩充。扩充后的数据集可以更好地训练一个拟合受害者模型决策边界的替代模型。其中，迭代的数据合成过程定义如下：

(3.4.6)¶\[\begin{aligned}D'_{t+1} = \{ {\boldsymbol{x}} + \lambda \cdot \text{sign}(J_{f'}[f({\boldsymbol{x}})]): {\boldsymbol{x}} \in D'_{t} \} \cup D'_{t}\end{aligned}\]

其中，\(\lambda\)表示步长，\(f'\)表示替代模型，\(J_{f'}\)表示基于黑盒目标模型\(f\)的输出计算得到的雅可比矩阵，\(\text{sign}(\cdot)\)表示符号函数，\(D'_{t}\)表示第\(t\)次迭代时得到的数据集。

式 (3.4.6) 的目的是合成更接近替代模型决策边界的样本，如果替代模型和受害者模型很接近，那么它也会更接近受害者模型的决策边界，这样的样本有助于替代模型进一步拟合受害者模型的决策边界。数据合成过程和替代模型的训练过程是交替进行的，和受害者模型相似的替代模型有助于合成的样本贴近受害者模型的决策边界，而贴近决策边界的合成样本进一步帮助替代模型模仿受害者模型。在替代数据集\(D'\)上训练得到最终的替代模型后，就可以利用已有白盒攻击算法（如FGSM和PGD）完成黑盒迁移攻击。

Knockoff Nets攻击（中文为“仿冒网络攻击”）是一种经典的模型抽取方法，其通过训练一个类似的模型来复制目标模型。Knockoff Nets攻击无须知道目标模型的先验信息，攻击者\(A\)只需构建迁移（替代）数据集\(D'(X)=\{({\boldsymbol{x}}_{i},f({\boldsymbol{x}}_{i}))\}_{i=1}^{m}\)，使迁移数据集无限逼近受害者模型的训练数据分布，之后使用迁移数据集训练得到一个与受害者模型功能相似的替代模型，从而实现模型抽取。

在Knockoff Nets攻击中，构建迁移数据集\(D'\)是最关键的一步，用于向目标模型发起查询。研究者在文中提出了两种构建策略：

随机策略：攻击者从一个大规模公开数据集（如ImageNet）分布中随机抽取样本\({\boldsymbol{x}} \stackrel{iid}{\sim} P_{A}(X)\)；
自适应策略：攻击者利用强化学习从大规模公开数据集中选择更有利于抽取的样本\({\boldsymbol{x}} \sim {\mathbb{P}}_{\pi}(\{{\boldsymbol{x}}_{i},y_{i}\}^{t-1}_{i=1})\)（\({\mathbb{P}}_{\pi}\)为强化学习得到的采样策略，\({\boldsymbol{x}}_i \sim P_A(X)\)）。

实验发现，哪怕是随机策略，只需要6万次查询便可以获得一个达到受害者模型（Resnet-34）90%功能的替代模型。

3.4.3. 基于元模型的抽取¶

基于元模型的抽取（Meta-Model Based Attack，MMBA） (Oh et al., 2019) 通过训练一个能够模仿目标模型行为的元模型，从而有效地窃取目标模型的功能。具体来说，攻击者\(A\)训练一个元模型\(\Phi(\cdot)\)，将受害者模型的预测输出\(f({\boldsymbol{x}})\)作为元模型的输入，并将受害者模型的参数信息作为元模型的输出\(\Phi(f({\boldsymbol{x}}))\)。为了构建元模型的训练数据集\(\{f({\boldsymbol{x}}),\Phi(f({\boldsymbol{x}}))\}\)，攻击者\(A\)需要准备大量与目标模型功能相似但具有不同属性的模型\(f \sim \mathcal{F}\)。经过多次训练之后，元模型\(\Phi(\cdot)\)就可以预测受害者模型\(f(\cdot)\)的属性信息，例如激活函数、网络层数、优化算法等信息。基于元模型的抽取攻击流程如图3.4.4 所示。

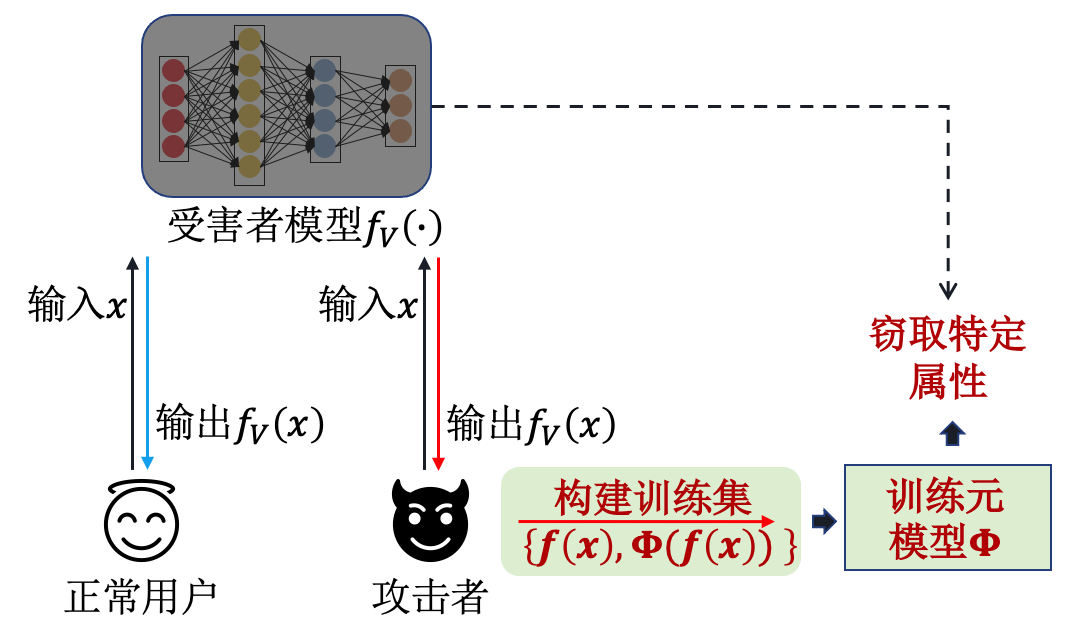
图3.4.4 基于元模型的抽取攻击流程图¶

元模型抽取攻击在MNIST数据集上成功抽取了受害者模型的属性信息，包括模型架构、优化器和数据信息。给定想要抽取的模型属性\(a\)，如激活函数、卷积核大小、批大小、数据大小等12个属性，元模型抽取攻击通过求解下面的优化问题来训练元模型：

(3.4.7)¶\[\begin{aligned}\min\limits_{\theta} \mathop{\mathbb{E}}\limits_{f \sim \mathcal{F}} \left[\sum^{12}_{a=1} \mathcal{L}_{CE} (\Phi^{a}_{\theta}([f({\boldsymbol{x}}_i)]^{n}_{i=1}), y^{a})\right]\end{aligned}\]

其中，\(\theta\)表示元模型的参数，\(\mathcal{F}\)表示元训练中模型的分布，\(a\)表示目标模型的属性，\(y^{a}\)表示模型属性的真实标签。上述损失函数\(\mathcal{L}_{CE}\)定义了输出受害者模型的属性信息\(\Phi^{a}{\theta}([f({\boldsymbol{x}}{i})]^{n}_{i=1})\)与受害者模型的真实属性信息\(y^{a}\)之间的距离。需要注意的是，构建元模型的训练数据集\({f({\boldsymbol{x}}),\Phi(f({\boldsymbol{x}}))}\)需要大量任务相关的数据和模型，有很大的人力和计算开销，因此在实际应用中存在一定的局限性。因此，这种方法的可行性和有效性取决于攻击者能否收集到足够多的与目标模型相关的数据和模型。

3.5. 数据抽取¶

数据抽取 2 （Data Extraction）是一种对目标模型进行逆向工程，抽取其原始训练数据的攻击。早期的数据抽取研究工作大都基于简单的图像分类模型进行，从训练好的图像分类模型中恢复用于训练模型的原始训练图像。

图像数据抽取最早是在2015年提出的，研究者通过在输入上进行梯度下降来获取类别图像。随后，有研究对该种方法进行了改进和扩展 (He et al., 2019, Yang et al., 2019) ，但这些方法只在浅层神经网络上证明了有效性或需要额外的信息才能够完成图像抽取。此外，研究者希望通过可视化神经网络来理解它们的属性。例如，通过对预训练模型进行逆向和激活最大化进行图像生成 (Mahendran and Vedaldi, 2015, Mahendran and Vedaldi, 2016) ；通过训练一个生成对抗网络（GAN）的生成器作为先验，并使用生成器训练卷积神经网络生成图像 (Nguyen et al., 2017, Nguyen et al., 2016) 。然而，这些方法仍依赖辅助数据集信息或额外的预训练模型,与现实应用场景仍有较大差距。

在没有辅助数据和额外信息的条件下，如何从一个训练好的模型中恢复训练数据？一个经典的方法是DeepDream (Mordvintsev et al., 2015) ，其持续修改一张随机噪声（或自然图片）图片使其最大化某个指定类别的神经激活，同时配合一些正则化项来生成一张“看上去还有点意义”的图像。这是一个可解释性方法，生成的图像解释了模型的决策原理或者学习到的某种概念。但是DeepDream生成的图像并不自然，很多时候非常抽象。在此基础上，来自英伟达的研究者提出了DeepInversion (Yin et al., 2020) 。他们发现当前广泛应用的深度网络都隐式编码了丰富的训练数据信息，并且这些网络都引入了批归一化层（Batch Normalization），它们存储了模型训练过程中很多层输出的均值和方差。基于这些均值和方差，DeepInversion为中间层的激活进行了一定的正则化，可以在不需要任何训练数据和额外信息的条件下进行图像合成，同时生成的图像保真度高，比较接近训练数据的原始分布。下面将对DeepDream和DeepInversion这两个代表性图像数据抽取方法进行详细介绍。

DeepDream (Mordvintsev et al., 2015) 采用优化的方式将一张噪声图片逐渐优化成来自训练集的一张自然图像。给定一张随机噪声图片输入\(\hat{{\boldsymbol{x}}} \in \mathbb{R}^{H \times W \times C}\)，其中\(H\)，\(W\)，\(C\)分别表示噪声的高度，宽度和颜色通道数。给定目标类别\(y\)，DeepDream通过下面的优化公式来合成图像：

(3.5.1)¶\[\min_{\hat{{\boldsymbol{x}}}} \mathcal{L}_{CE}(\hat{{\boldsymbol{x}}}, y) + R(\hat{{\boldsymbol{x}}})\]

其中，\(\mathcal{L}_{CE}(\cdot)\)是交叉熵损失函数，\(R(\cdot)\)是图像正则化项。DeepDream使用图像先验来引导\(\hat{{\boldsymbol{x}}}\)远离不真实图片：

(3.5.2)¶\[R_{prior}(\hat{{\boldsymbol{x}}}) = \alpha_{tv} R_{tv}(\hat{{\boldsymbol{x}}}) + \alpha_{\ell_2} R_{\ell_2}(\hat{{\boldsymbol{x}}})\]

其中，\(R_{tv}\)和\(R_{\ell_2}\)分别是\(\hat{{\boldsymbol{x}}}\)的总变差（total variation）和\(L_2\)范数的正则化项，变量\(\alpha_{tv}\)和\(\alpha_{\ell_2}\)是对应的缩放因子。图像先验正则化能够帮助图像更加稳定的收敛得到一个有效的自然图像，只是这些图像仍与原始训练图像有着巨大差距。

DeepInversion 是一种基于知识蒸馏 (Hinton et al., 2015) 的数据抽取方法。知识蒸馏是两个模型之间的知识迁移，从一个大的教师模型（teacher model）迁移到一个小的学生模型（student model）。这种方法的核心思想是利用教师模型的输出（通常是概率分布，也称为“软标签”）来指导训练学生模型。在知识蒸馏过程中，教师模型的输出可以通过一个温度参数进行平滑，较高的温度会产生一个更加平滑的软标签分布，而较低的温度会使分布更接近硬标签。通过结合软标签和温度平滑，学生模型可以学习到教师模型的一些细微的、难以用硬标签表示的知识。

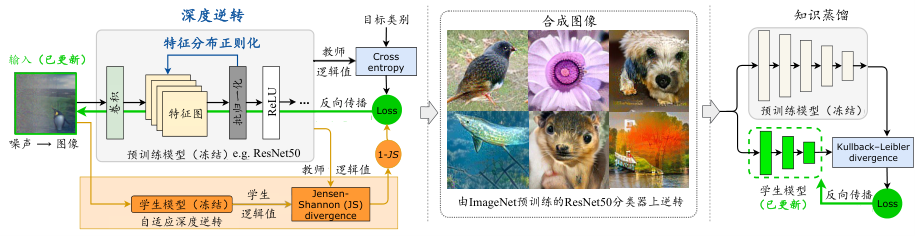
图3.5.1 DeepInversion抽取流程图 (Yin et al., 2020)¶

DeepInversion的实现方法如图3.5.1 所示。给定一个预训练模型\(p_T(x)\)和一个数据集\(\chi\)，学生模型的参数\(W_S\)，学生模型可以通过以下公式进行学习：

(3.5.3)¶\[\min_{W_S} \sum_{{\boldsymbol{x}} \in \chi} KL(p_T({\boldsymbol{x}}), p_S({\boldsymbol{x}}))\]

其中，\(KL(\cdot)\)是KL（Kullback-Leibler）散度，\(p_T({\boldsymbol{x}}) = p({\boldsymbol{x}}; W_T)\)和\(p_S({\boldsymbol{x}}) = p({\boldsymbol{x}}; W_S)\)是教师模型和学生模型的输出概率分布。

DeepInversion提出一个新的特征分布正则化项来提高生成图像的质量。为了有效匹配合成图像\(\hat{{\boldsymbol{x}}}\)和原始图像\({\boldsymbol{x}}\)的各层次特征，DeepInversion提出最小化\(\hat{{\boldsymbol{x}}}\)和\({\boldsymbol{x}}\)之间的特征图统计信息距离。假设特征统计信息遵循跨批次（batch）的高斯分布，因此可以通过均值\(\mu\)和方差\(\sigma^2\)来定义。特征分布正则化项可定义为：

(3.5.4)¶\[R_{feature}(\hat{{\boldsymbol{x}}}) = \sum_l \left \| \mu_l(\hat{{\boldsymbol{x}}}) - \mathbb{E}[\mu_l({\boldsymbol{x}})|\chi] \right \|_2 + \sum_l \left \| \sigma^2_l(\hat{{\boldsymbol{x}}}) - \mathbb{E}[\sigma^2_l({\boldsymbol{x}})|\chi] \right \|_2\]

其中，\(\mu_l(\hat{{\boldsymbol{x}}})\)和\(\sigma^2_l(\hat{{\boldsymbol{x}}})\)是对应第\(l\)个卷积层特征图的批均值和批方差的估计值。\(\mathbb{E}[\cdot|\chi]\)和\(\left \| \cdot \right \|_2\)分别表示给定\(\chi\)条件下的期望值和\(L_2\)范数。

通过上述公式可知，我们需要得到训练图像的\(\mathbb{E}[\mu_l({\boldsymbol{x}})|\chi]\)和\(\mathbb{E}[\sigma^2_l({\boldsymbol{x}})|\chi]\)。巧妙的是，这两个信息就在模型的批归一化层里。因此，公式 (3.5.4) 中的期望和方差可以近似为:

(3.5.5)¶\[E[\mu_l({\boldsymbol{x}})|\chi] \approx BN_l(\text{running_mean})\]

(3.5.6)¶\[E[\sigma^2_l({\boldsymbol{x}})|\chi] \approx BN_l(\text{running_variance})\]

将特征分布正则化项融合到公式 (3.5.1) 的正则化项\(R(\cdot)\)中，可以得到DeepInversion的完整正则化项：

(3.5.7)¶\[R_{DI}(\hat{{\boldsymbol{x}}}) = R_{prior}(\hat{{\boldsymbol{x}}}) + \alpha_f R_{feature}(\hat{{\boldsymbol{x}}})\]

特征分布正则化显著提高了生成图像的质量。但是除了提高生成图像的质量，避免生成图像的冗余也至关重要。对此，研究者进一步提出了Adaptive DeepInversion方法，通过增加教师和学生模型之间的竞争激励，使生成的图像更加多样化。具体来说，Adaptive DeepInversion引入了基于JS（Jensen-Shannon）散度的正则项\(R_{compete}\)来惩罚输出分布的相似性：

(3.5.8)¶\[\begin{split}R_{compete}(\hat{{\boldsymbol{x}}}) & = 1 - JS(p_T(\hat{{\boldsymbol{x}}}), p_S(\hat{{\boldsymbol{x}}})) \\JS(p_T(\hat{{\boldsymbol{x}}}), p_S(\hat{{\boldsymbol{x}}})) & = \frac{1}{2} \left( KL(p_T(\hat{{\boldsymbol{x}}}), M) + KL(p_S(\hat{{\boldsymbol{x}}}), M) \right)\end{split}\]

其中，\(M = \frac{1}{2} \cdot (p_T(\hat{{\boldsymbol{x}}}) + p_S(\hat{{\boldsymbol{x}}}))\)是教师和学生输出分布的均值。 Adaptive DeepInversion的正则化项包括：

(3.5.9)¶\[R_{ADI}(\hat{{\boldsymbol{x}}}) = R_{DI}(\hat{{\boldsymbol{x}}}) + \alpha_c R_{compete}(\hat{{\boldsymbol{x}}})\]

其中，\(\alpha_c\)为调和系数。如图3.5.2 所示，Adaptive DeepInversion通过竞争激励，迭代提升学生模型生成图像的多样性，逐步扩大了生成图像的覆盖范围，有效促进了新图像的出现，是DeepInversion的增强版。

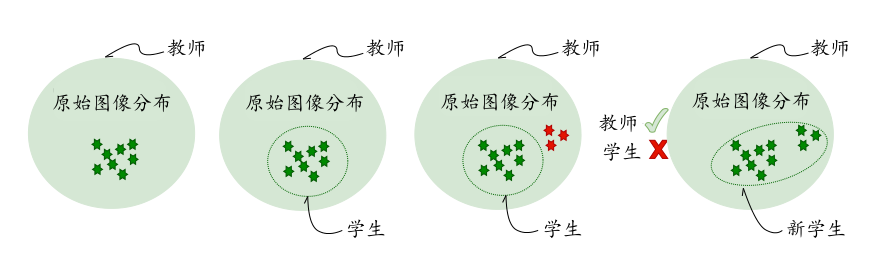
图3.5.2 Adaptive DeepInversion提高生成图像多样性的竞争方案 (Yin et al., 2020)¶

3.6. 成员推理¶

随着数据量的不断增加和人工智能的迅猛发展，数据隐私已成为日益重要的议题。特别是在机器学习领域，模型可能无意中记忆并泄露有关训练数据的敏感信息，从而引发严重的隐私泄漏问题。在这样的大背景下，成员推理攻击（Membership Inference Attack，MIA）应运而生。作为一种新型的隐私攻击方式，成员推理攻击通过判定某个样本是不是被模型训练过，即其是否为训练数据集中的一员，来嗅探有关训练数据的隐私信息。此类攻击揭示了机器学习模型存在的隐私泄露风险。通过成员推理攻击，攻击者有可能推断出某人是否患有某种难以启齿的疾病，或者是否去过某个特殊的场所，引发严重的隐私问题。

直观来讲，相比没有训练过的样本，模型在训练过的样本上的损失和梯度信息肯定会有所不一样。因此，成员推理攻击可以根据模型在训练与测试样本上的输出差异来判定某个样本是否属于训练集。为此，攻击者需要构造一个攻击模型（attack model）去自动识别这种差异，并且需要构造类似的数据来训练这个攻击模型。一个经典的成员推理攻击方法基于所谓“影子模型”来进行攻击，此方法通过构建并训练一系列影子模型来模拟目标模型的行为，进而训练出一个能够高效执行成员推理攻击的攻击模型。这种攻击的有效性通常依赖于模型对训练数据和未见数据的行为差异，以及模型过拟合的程度。影子模型方法不仅提高了攻击的准确性，而且揭示了模型在训练数据隐私方面的安全隐患，需要在设计和部署人工智能模型时采取必要措施严加防范。

下面将详细介绍基于影子模型的成员推理攻击算法，包括问题设置、影子模型、攻击模型和评价指标。

3.6.1. 问题设置¶

以基于深度神经网络的图像分类模型为例，将图像样本空间表示为 \({\mathcal{X}}\)，每幅图像\({\boldsymbol{x}}\)对应的类别标签为\(y \in \{1, 2, \dots, C\}\)，其中\(C\)为类别总数。一个具有参数\(\theta\)的分类模型\(f_\theta: {\mathcal{X}} \to {\mathcal{Y}}\)将输入图像\({\boldsymbol{x}} \in {\mathcal{X}}\)映射为\(C\)维置信度向量\(p = f_\theta({\boldsymbol{x}}) \in {\mathcal{Y}}\) 其中，\({\mathcal{Y}} = [0, 1]^C\)表示输出空间。训练集 \(D\)由\({\mathcal{X}}\)中（在服从样本概率分布的前提下独立同分布地）随机抽取得到的元素构成，模型\(f\)的训练目标为最小化在训练集\(D\)上的经验损失：

(3.6.1)¶\[\min_{\theta}\ \ \frac{1}{|D|} \sum_{({\boldsymbol{x}}, y) \in D} \mathcal{L}(f_\theta({\boldsymbol{x}}), y)\]

其中，损失函数\(\mathcal{L}\)为常用的交叉熵损失函数\(\mathcal{L}(f_\theta({\boldsymbol{x}}), y)=-\log (p_y)\)。

在模型训练过程中，一般采用随机梯度下降法对模型参数 \(\theta\) 进行优化：

(3.6.2)¶\[\theta_{t + 1} = \theta_t - \eta \cdot \nabla_{\theta} \left( \frac{1}{|B_t|} \sum_{({\boldsymbol{x}}, y) \in B_t} \mathcal{L}(f_{\theta_t}({\boldsymbol{x}}), y) \right)\]

其中， \(\eta\)为学习率，\(B_t\)为第\(t\) 步迭代的小批量样本。

下面的挑战游戏定义了一般的成员推理攻击：

定义 3.1（成员推理挑战游戏）给定样本空间 \({\mathcal{X}}\)及分布，成员推理挑战游戏在一名挑战者（challenger）\(\mathcal{C}\)和一名对抗者（adversary）\(\mathcal{A}\) 之间进行：

挑战者从 \({\mathcal{X}}\)中随机采样得到训练集\(D\)，并在其上训练一个分类模型\(f_\theta\)；
挑战者随机抽取一位比特 \(b\)，若\(b = 1\)则从\(D\)中随机抽取一个样本，若\(b = 0\)则从\({\mathcal{X}} \setminus D\)中随机抽取一个样本，记抽取到的样本为\(({\boldsymbol{x}}, y)\)；
挑战者向对抗者发起挑战，要求对抗者判断样本 \(({\boldsymbol{x}}, y)\)是否属于训练集\(D\)；
对抗者 \(\mathcal{A}\)利用样本空间\({\mathcal{X}}\)及分布的先验知识和对模型\(f_\theta\)的访问权限对\(({\boldsymbol{x}}, y)\)是否属于\(D\)进行判断，若判断\(({\boldsymbol{x}}, y)\)属于\(D\)则输出比特\(\hat{b} = 1\)，否则输出比特\(\hat{b} = 0\)；
若 \(\hat{b} = b\)则对抗者挑战成功，最终挑战结果为\(1\)，否则挑战失败，最终结果为\(0\)。

3.6.2. 影子模型¶

基于影子模型（shadow model）的成员推理攻击算法 (Shokri et al., 2017) 是最经典的成员推理攻击方法。此攻击算法的思想是，通过训练一系列模仿目标模型行为的“影子模型”来构造攻击模型（最终用来判定一个样本是否属于训练集的模型）。最终的攻击模型是一系列模型的集合，每个模型对应一个类别。之所以将攻击模型设置为类别模型的集合是因为，有时候类别间的差异甚至大过训练集与测试集之间的差异，所以成员推理需要一个类别一个类别的进行。影子模型也是需要训练的，其训练集也是逐类别构造的。

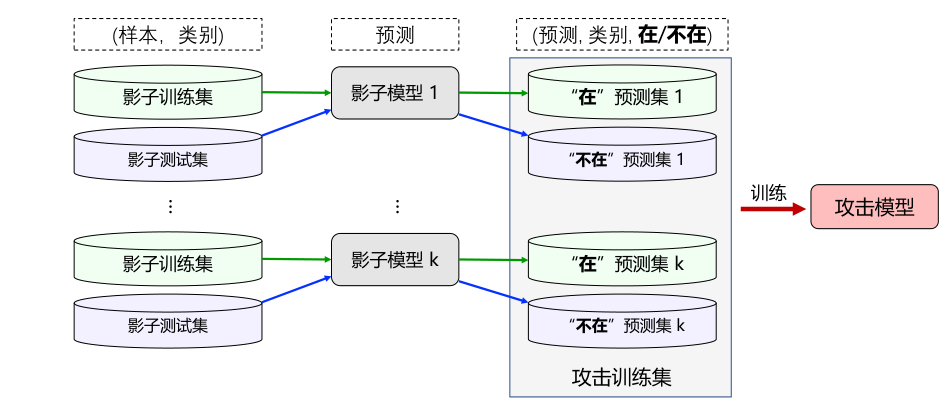
图3.6.1 基于影子模型的成员推理攻击方法 (Shokri et al., 2017)¶

为了训练影子模型，攻击者首先需要获得一些与真实训练集独立同分布的训练样本。本小节介绍一种基于模型的（model-based）概率性数据合成方法，通过调用目标模型的 API 进行采样以合成影子模型的训练数据，详细流程如算法图3.6.2 所示。

首先在开始合成前需要确定所要合成样本的类别 \(c\)；从每轮迭代（第 6 行）开始，将上一轮迭代生成的“候选”样本\({\boldsymbol{x}}\)送入目标模型\(f_{\theta}\)得到置信度向量\(p\)，随后对目标类别的置信度\(p_c\) 进行分情况讨论：
1. 若 \(p_c\)超过历史最高置信度\(p_c^*\)（第 8 行），则此时算法暂不将其设置为新的历史最高置信度，而是先判断其是否已满足合成数据的要求——若置信度\(p_c\)不仅超过最低容忍置信度\(conf_{min}\)，同时还是所有类别置信度中的最高者，那么算法便以概率\(p_c\)返回该样本；若该样本未被返回或并未满足合成数据的要求，则将新的历史最高置信度\(p_c^*\)设置为\(p_c\)，并将新的历史最佳合成样本\({\boldsymbol{x}}^*\)设置为\({\boldsymbol{x}}\)，然后继续迭代。
2. 若 \(p_c\)并未超过历史最高置信度，那么算法将进入所谓的“评估阶段”（第 16 行以后）。这里的核心步骤是对当前的历史最佳合成样本\({\boldsymbol{x}}^*\)的\(k\)个特征进行随机扰动（第 21 行）。如果扰动的样本不符合条件则拒绝加一，如果拒绝次数超过最大容忍连续拒绝次数\(rej_{max}\)，则对采样特征数\(k\)进行减半（直至\(k\)减小到最低容忍随机特征数\(k_{min}\) 为止，此时保持固定，不再减半）。每次减半都会重置拒绝次数。
整体算法进行迭代，直到达到最大迭代次数 \(T\)，此时将返回最终结果“拒绝（\(\bot\)）”。

为了确保本算法能很好地运行，我们需要随机采样能够有效率地探索样本空间并且对其进行分类。因此，样本空间过大（例如图像的分辨率较高，即样本空间维数较高）或者目标模型的计算速度慢（例如该模型的分类任务较为复杂）都会对算法的执行效率和结果造成消极影响。

图3.6.2 利用目标模型合成训练数据¶

3.6.3. 攻击模型¶

攻击模型的训练过程如下：

首先确定攻击模型训练集的大小—，训练集需要包含所有标签（\(in\)和\(out\)），并且每个标签下的样本数相同。
使用算法图3.6.2 采样训练集，并将训练集等量分割用于训练各影子模型，分割的训练子集进而被一分为二，分别作为影子模型的训练集和测试集。
在各训练子集上训练各影子模型，并获取其对每个样本的预测概率向量。攻击模型的训练集由影子模型的训练/测试集样本与和对应的概率向量组成（并被标记为\(in\)和\(out\)标签）。
将上一步得到的训练样本重新合并为一个整体，并根据类别平均分为 \(c_{target}\) 个子集。
针对每个目标类别训练一个对应的攻击模型用于对该类别的样本进行成员推断，即最终会产生\(c_{target}\) 攻击模型。

若假设目标模型为已知，则攻击模型应利用目标模型的训练集样本的概率向量进行训练、捕捉目标模型分别在对待训练集样本时和对待测试集样本时的区别；而改为使用影子模型后就转变为了使用影子模型的概率向量训练捕捉影子模型对待从目标模型中采样得到的训练/测试集样本的区别。前后两个场景之间不同概念的转变有两处近似：一是“人类觉得同属于一个类别的图像”转变为“目标模型觉得同属于一个类别的图像”；二是“目标模型对待训练集和测试集的区别”转变为“影子模型对待训练集和测试集的区别”。其中后一种近似要求目标模型和影子模型的结构和大小相近，而前一种近似则要求样本合成算法图3.6.2 （通过目标模型）得到的训练集的分布和从实际人眼得到的训练集的分布相近。直觉上只要目标和影子模型（分类器）的结构、大小、训练方式以及目标和影子训练集、测试集的分布均趋于一致，攻击模型在目标模型和影子模型上学习到的二分类决策也会趋于一致。对于训练集和测试集的分布，研究人员假设目标模型在其私有训练集样本上的概率预测向量的各个分量的取值满足“某一个类别占绝大部分概率”的分布，并假设根据该分布采样得到的样本的分布与目标模型私有训练集样本的分布是相似的。模型结构、大小或是训练/测试集样本是否完全相同并不是决定影子训练方法成功与否的关键，如何逼近目标模型学习到的特征在区分训练集和测试集时的区别才是。

3.6.4. 评价指标¶

成员推理攻击本质上是对目标样本的二分类判断，所以最差情况为随机猜测，即准确率为50%。对于单次实验，可以使用精准度和召回率来衡量攻击效果，对于多次实验，可以绘制 ROC 曲线并计算 AUC值。此外，评估时攻击效果时需要每个类别单独衡量，这是因为类间差异较大，样本数不均衡，影子和攻击模型的拟合程度也不相同。

3.7. 本章小结¶

本章系统介绍了针对小模型所提出的对抗攻击、数据投毒、后门攻击、模型抽取、数据抽取和成员推理六类攻击算法。其中在对抗攻击方面，介绍了白盒攻击、黑盒攻击和物理攻击，并详细讨论了相关算法的设计思路和攻击步骤；在数据投毒方面，介绍了标签投毒、在线投毒、特征空间投毒以及基于优化和生成的投毒攻击算法；在后门攻击方面，介绍了输入空间攻击、参数空间攻击、特征空间攻击、迁移学习攻击和联邦后门攻击，揭示模型在开发生命周期不同环节中所面临的投毒风险；在模型抽取方面，介绍了基于方程式求解、替代模型、Knockoff Nets以及原模型的抽取策略；在数据抽取方面，介绍了DeepDream和DeepInversion两个经典算法；在成员推理方面，详细介绍了基于模型过拟合性质和影子模型的攻击算法思想。通过这些攻击算法，我们可以了解到攻击小模型的各种可能，揭示了小模型所广泛存在的脆弱性。这些攻击算法可以用来评估模型的安全性，同时协助我们进行防御技术的开发。

3.8. 习题¶

列举三个白盒对抗攻击算法并写出它们的对抗样本生成公式。
列举两个迁移对抗攻击需要解决的技术难题和可能的解决方案。
阐述数据投毒和后门攻击的不同，并列举三种数据投毒的可行思路。
描述后门攻击的一般流程并解释说明后门攻击为什么不会影响模型性能。
简述模型抽取攻击与知识蒸馏之间的联系和区别。
解释说明在什么情况下模型更容易泄露原始训练数据。

1: 模型抽取攻击也经常被称为“模型窃取”攻击，本书建议使用比较中性的“模型抽取”来描述这一类攻击算法。
2: 数据抽取也叫“模型逆向”或者“数据窃取”，本书建议使用相对中性的“数据抽取”来描述此类攻击。